高中数学 第2章 解三角形 213 正、余弦定理的应用课件 北师大版必修5 课件VIP免费

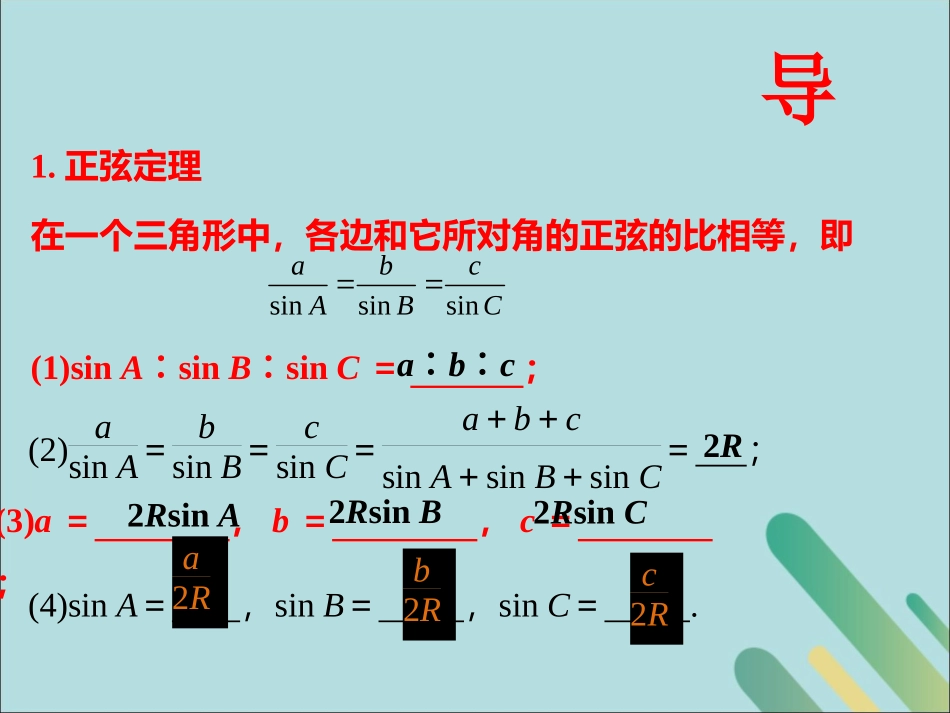
§2.1.2正、余弦定理的应用学习目标：1.熟记余弦定理并能灵活变形应用；2.能灵活应用边角互化解三角形即判断三角形的形状等.1.正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即(1)sinA∶sinB∶sinC＝；a∶b∶c(2)asinA＝bsinB＝csinC＝a＋b＋csinA＋sinB＋sinC＝；2R(3)a＝，b＝，c＝；2RsinA2RsinB2RsinC(4)sinA＝，sinB＝，sinC＝.a2Rb2Rc2RsinsinsinabcABC导2.余弦定理的内容：2222cosbacacB2222cosabcbcA2222coscababC222cos2bcaAbc222cos2acbBac222cos2abcCab导1.在△ABC中，有a2-c2+b2=ab,则角C=_____;解析：由余弦定理知：222cos2abcCab又已知a2-c2+b2=ab所以2221cos222abcabCabab所以3C3思2.设2a+1,a,2a-1为钝角三角形的三边，求实数a的取值范围.解：思例1在△ABC中，已知(sinA＋sinC)(sinA－sinC)＝sinB(sinB＋sinC)，求角A的值.所以sin,sin,sin222abcABCRRR解析：由正弦定理知：2sinsinsinabcRABC所以原式可化为：()()()2222222acacbbcRRRRRRR消去R得()()()acacbbc即222acbbc222bcabc所以2221cos22bcaAbc即23A议、展解析：由正弦定理知：2sinsinsinabcRABC所以sin,sin,sin222abcABCRRR所以已知条件可转化为：::5:7:8222abcRRR消去R得::5:7:8abc设5,7,8,akbkck所以222222(5)(7)(8)1cos22577abckkkCabkk所以三角形为锐角三角形变式在△ABC中，若sinA：sinB：sinC=5:7:8，则三角形的最大内角的余弦值为______,三角形的形状为_____________.则角C为最大角，议、展所以2sin,2sinaRAbRB解析：(方法一：边化角)由正弦定理知：2sinsinsinabcRABC所以已知条件可转化为：2sincos2sincosRBARAB消去R并移项得sincossincos0BAAB即sin()0BA所以三角形为等腰三角形所以A=B例2在△ABC中，bcosA=acosB,判断三角形ABC的形状.又因为角A，B为三角形的内角议、展方法2:角化边根据bcosA=acosB，由余弦定理得acbcaabcacbb22222222整理为b2+c2-a2=a2+c2-b2即a=b故此三角形为等腰三角形议、展所以2sin,2sinaRAbRB解析：(边化角)由正弦定理知：2sinsinsinabcRABC所以已知条件可转化为：2sincos2sincosRAARBB消去R并变形得sin2sin2BA所以三角形为等腰三角形,或直角三角形。所以A=B或2A+2B=π又因为角A，B为三角形的内角变式在△ABC中，acosA=bcosB,判断三角形ABC的形状.所以A=B或A+B=½π议、展•[方法总结]判断三角形的形状，应围绕三角形的边角关系进行思考，主要看其是否是正三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形，要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别．依据已知条件中的边角关系判断时，主要有如下两条途径：评•(1)利用正、余弦定理把已知条件转化为边边关系，通过因式分解、配方等得出边的相应关系，从而判断三角形的形状；•(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系，通过三角函数恒等变形，得出内角的关系，从而判断出三角形的形状，此时要注意应用A＋B＋C＝π这个结论，在两种解法的等式变形中，一般两边不要约去公因式，应移项提取公因式，以免漏解．评即cosbAc解析：21coscos22AA(方法1：角化边)2222bbcacbc又222cos2bcaAbc所以为直角三角形。(方法2：边化角)由正弦定理知：即a2+b2=c21.在△ABC中，(a,b,c分别为角A,B,C的对边),判断三角形ABC的形状.2cos22Abcc1cos12222AbcbccsincossinbBAcC即cossinsinACB即cossinsin[()]sin()ACACACcossinsincoscossinACACAC即sincos0ACcos0C2C所以为直角三角形。检