高中数学 151曲边梯形的面积课件 新人教A版选修2-2 课件VIP免费

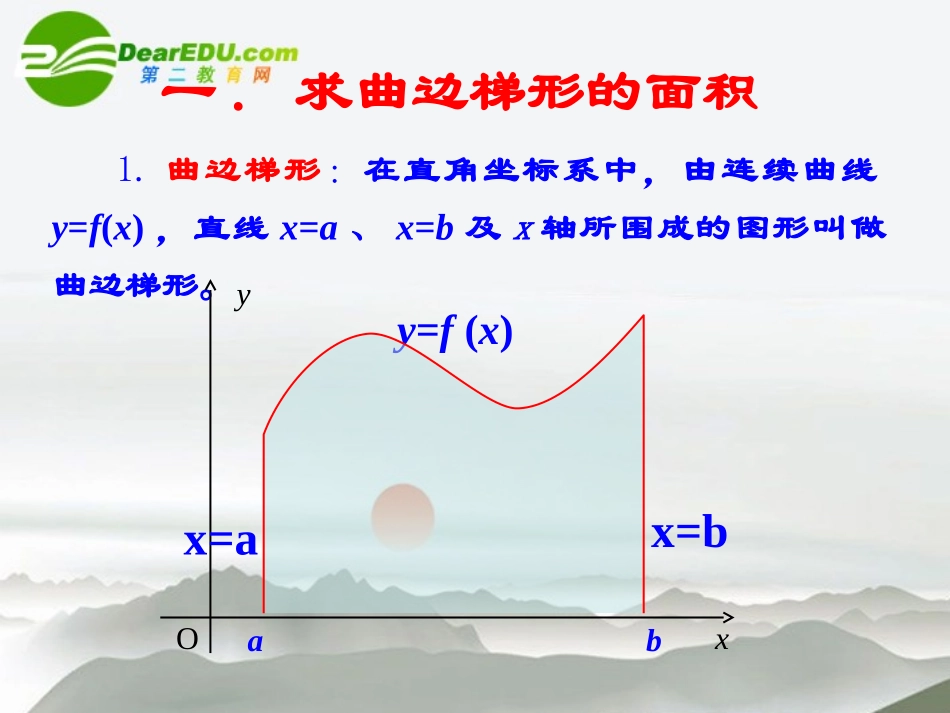
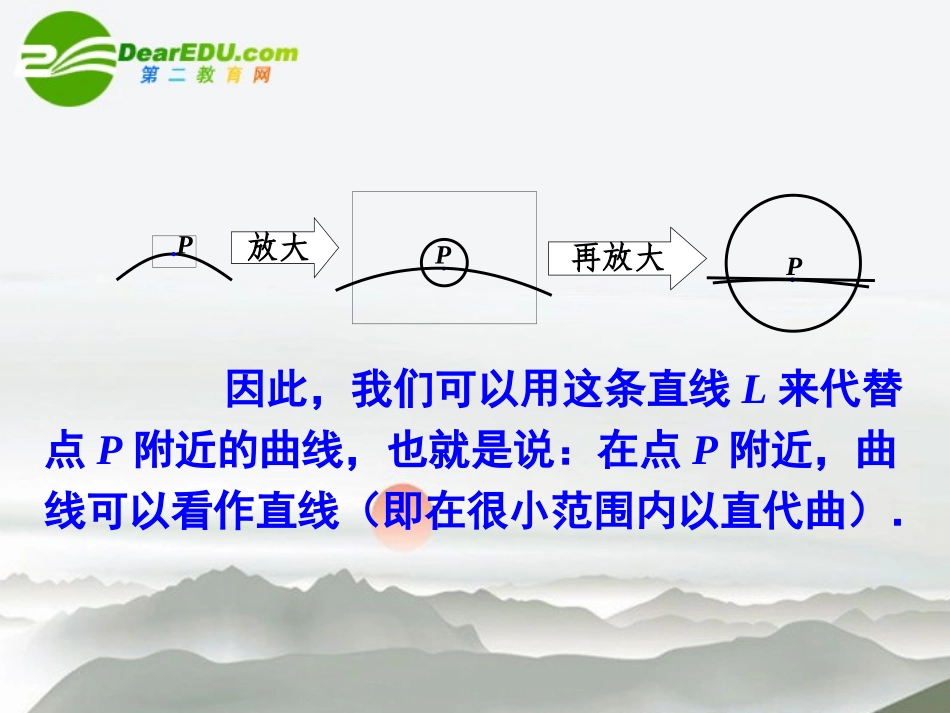
1.5.1曲边梯形的面积1.曲边梯形：在直角坐标系中，由连续曲线y=f(x)，直线x=a、x=b及x轴所围成的图形叫做曲边梯形。Oxyaby=f(x)一.求曲边梯形的面积x=ax=b因此，我们可以用这条直线L来代替点P附近的曲线，也就是说：在点P附近，曲线可以看作直线（即在很小范围内以直代曲）．P放大再放大PPy=f(x)baxyOA1AA1.用一个矩形的面积A1近似代替曲边梯形的面积A，得AA1+A2用两个矩形的面积近似代替曲边梯形的面积A，得y=f(x)baxyOA1A2AA1+A2+A3+A4用四个矩形的面积近似代替曲边梯形的面积A，得y=f(x)baxyOA1A2A3A4y=f(x)baxyOAA1+A2++An将曲边梯形分成n个小曲边梯形，并用小矩阵形的面积代替小曲边梯形的面积，于是曲边梯形的面积A近似为A1AiAn——以直代曲,无限逼近（1）分割把区间[0，1]等分成n个小区间：],nn,n1n[,],ni,n1i[,],n2,n1[],n1,0[n1n1inix每个区间的长度为过各区间端点作x轴的垂线，从而得到n个小曲边梯形，他们的面积分别记作.S,,S,,S,Sni21n1n2nknnxOy2xy例1.求抛物线y=x2、直线x=1和x轴所围成的曲边梯形的面积。（2）近似代替n1)n1i(x)n1i(fS2i（3）求和])1n(210[n1n1)n1-i(n1)n1-if(SSSSS22223n1i2n1in1iin21(不足近似值)（4）取极限1111(1)(2)6nn31S.3S所以2222(1)(21)1236nnnn311111(n1)n(2n1)(1)(2)n66nnS当分割的份数无限增多,即n→∞,△x→0时区间[0，1]的等分数nS的近似值20.1250000040.2187500080.27343750160.30273450320.31787109640.325561521280.329437262560.331382755120.3323574110240.3328452120480.33308923……nS我们还可以从数值上可以看出这一变化趋势（请见表）n1n2nknnxy2xynnn2ii1i1i12222311SSf()()nnnn1[12(n1)]niin(过剩近似值)n1n2nknnxy2xy2222331S[12(n1)]n1(1)(21)1111(1)(2)n663nnnnnn(过剩近似值)小结:求由连续曲线yf(x)对应的曲边梯形面积的方法（1）分割（2）近似代替（4）取极限n（3）求和1.当n很大时，函数在区间上的值，可以用()近似代替A.B.C.D.2)(xxfnini,1C)1(nf)2(nf)(nif0f练习2、在“近似代替”中，函数f(x)在区间上的近似值等于（）A.只能是左端点的函数值B.只能是右端点的函数值C.可以是该区间内任一点的函数值D.以上答案均不正确)(ixf)(1ixf),)((1iiiixxfC1,iixx练习作业P42练习题