高考数学总复习 2.5二次函数课件 文 大纲人教版 课件VIP免费

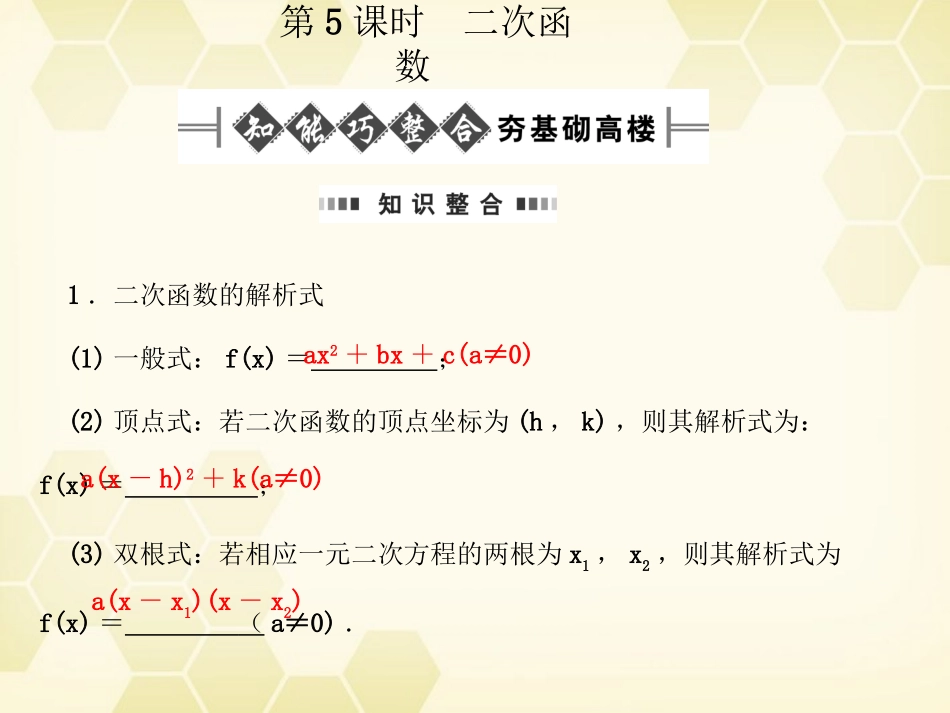
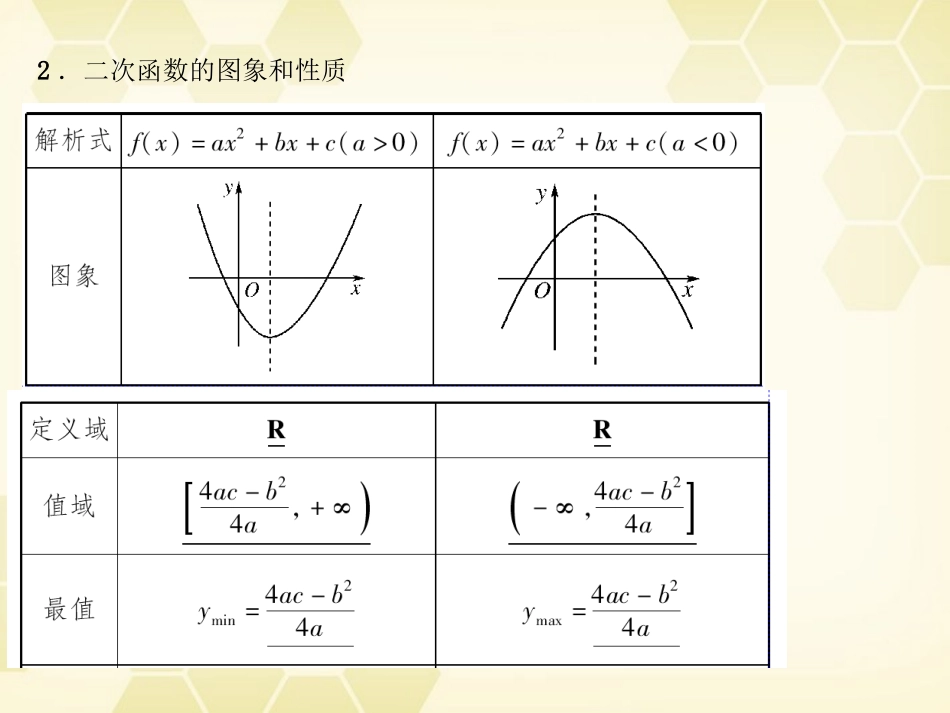
第5课时二次函数1．二次函数的解析式(1)一般式：f(x)＝；(2)顶点式：若二次函数的顶点坐标为(h，k)，则其解析式为：f(x)＝；(3)双根式：若相应一元二次方程的两根为x1，x2，则其解析式为f(x)＝（a≠0)．ax2＋bx＋c(a≠0)a(x－h)2＋k(a≠0)a(x－x1)(x－x2)2．二次函数的图象和性质1．函数y＝－x2(x∈R)是()A．左减右增的偶函数B．左增右减的偶函数C．减函数，奇函数D．增函数，奇函数答案：B解析：答案：C答案：D解析：答案：9或255．若函数f(x)＝x2＋(a＋2)x＋b(x∈[a，b])的图象关于直线x＝1对称，则f(x)max＝________.解析：答案：30求二次函数解析式的方法：待定系数法．根据所给条件的特征，可选择一般式、顶点式或两点式中的一种来求．利用已知条件求二次函数解析式常用的方法是待定系数法，但可根据具体的条件选用适当形式的解析式．(1)已知三个点的坐标时，宜用一般式；(2)已知拋物线的顶点坐标或与对称轴有关或与最大(小)值有关时，常使用顶点式；(3)若已知拋物线与x轴有两个交点，且横坐标已知时，选用两点式求f(x)更方便．解析：[变式训练]1.已知f(x)是二次函数，不等式f(x)＜0的解集是(0,5)，且f(x)在区间[－1,4]上的最大值是12.求f(x)的解析式．解析：∵f(x)是二次函数，且f(x)＜0的解集是(0,5)，∴可设f(x)＝ax(x－5)(a＞0)．∴f(x)在区间[－1,4]上的最大值是f(－1)＝6a.由已知，得6a＝12，∴a＝2.∴f(x)＝2x(x－5)＝2x2－10x(x∈R)．二次函数求最值问题，首先采用配方法化为y＝a(x－m)2＋n的形式，得顶点(m，n)和对称轴方程x＝m，结合二次函数的图象求解，常见有三种类型：(1)顶点固定，区间也固定；(2)顶点含参数(即顶点为动点)，区间固定，这时要讨论顶点横坐标何时在区间之内，何时在区间之外．(3)顶点固定，区间变动，这时要讨论区间中的参数．讨论的目的是确定对称轴和区间的关系，明确函数的单调情况，从而确定函数的最值．函数f(x)＝x2－2x＋2在闭区间[t，t＋1](t∈R)上的最小值记为g(t)．试写出g(t)的函数表达式．解析：∵f(x)＝x2－2x＋2＝(x－1)2＋1，当t＋1＜1，即t＜0时，函数在[t，t＋1]上为减函数，g(t)＝f(t＋1)＝t2＋1；当0≤t＜1时，g(t)＝f(1)＝1；当t≥1时，函数在[t，t＋1]上为增函数，g(t)＝f(t)＝t2－2t＋2.[变式训练]2.已知函数f(x)＝－x2＋2ax＋1－a在x∈[0,1]时有最大值2，求a的值．解析：函数f(x)＝－x2＋2ax＋1－a＝－(x－a)2＋a2－a＋1对称轴方程为x＝a.(1)当a＜0时，f(x)max＝f(0)＝1－a，∴1－a＝2，∴a＝－1.二次函数常和二次方程、二次不等式结合在一起．三个“二次”以二次函数为核心，通过二次函数的图象贯穿为一体，因此，解题时通过画二次函数的图象来探索解题思路是非常行之有效的方法．对于通过换元可转化为二次函数的问题，要注意中间换元的取值范围，它是转化后二次函数的定义域．已知方程x2－2ax＋4＝0，(1)若方程的两根，一根大于1，一根小于1，求实数a的取值范围；(2)若方程的两根均大于1，求实数a的取值范围．解析：解析：1．二次函数图象的对称轴是一条重要的直线，是增区间和减区间的分“”“”界线，在给定区间求最值和由根的分布求参数的范围等题型中都有重要的作用．通过对近三年高考试题的统计分析，有以下的命题规律：1“”．考查热点：二次函数的性质及应用，尤其是三个二次的综合应用，常与数形结合和等价转化思想联系在一起．2．考查形式：选择题、填空题、解答题均可能出现．3．考查角度：一是以二次函数的图象为载体，利用数形结合的思想，解决二次函数的单调区间、最值问题及与此有关的参数范围问题．二是一元二次方程根的分布问题．三是考查二次函数、二次方程及二次不等式的关系，其中以二次函数为核心，通过二次函数的图象贯穿始终．4．命题趋势：与其他初等函数复合在一起考查函数的性质．因三次函数的导函数为二次函数，所以与导数结合在一起也是高考的命题方向．12分2009·江苏卷a为实数，函数fx＝2x2＋x－a·|x－a|.1若f0≥1，求a的取值范围；2求fx的最小值．规范解答：1因为f0＝－a|－a|≥1.所以－a＞0，即a＜0.由a2≥1知a≤－1，因此，a的取值范围为－∞，－1].4分解析：答案：A解析：答案：D练规范、练技能、练速度