高一数学正弦函数、余弦函数的性质 新课标 人教版 课件VIP免费

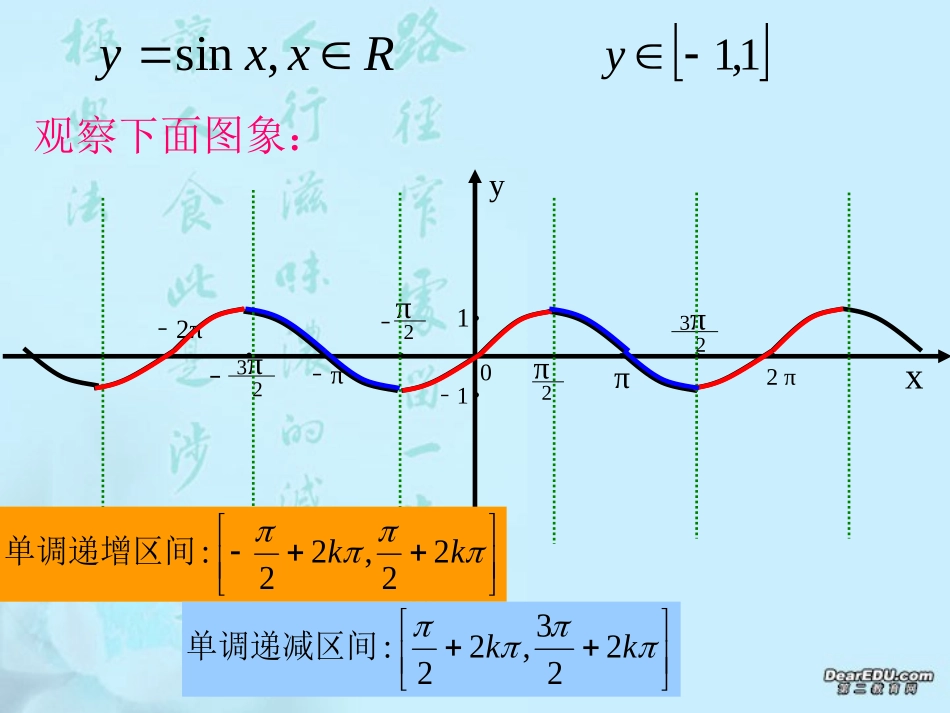
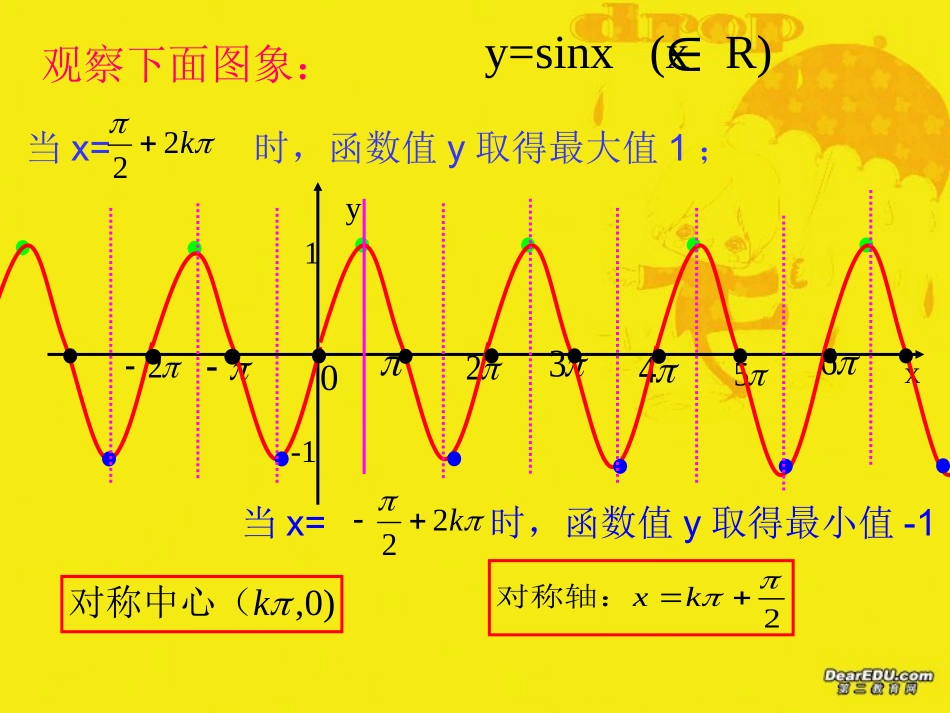
0π2π3π22π●●●●●●●●●﹣π2﹣π3π2﹣﹣2π1﹣1xykk22,22:单调递增区间Rxxy,sin1,1ykk223,22:单调递减区间观察下面图象：yx2346021-15y=sinx(xR)当x=时，函数值y取得最大值1；k22当x=时，函数值y取得最小值-1k22)0,k对称中心（2kx对称轴：观察下面图象：0π2π3π22π●●●●●●●●●﹣π2﹣π3π2﹣﹣2π1﹣1xykk2,2:单调递增区间Rxxy,cos1,1ykk2,2:单调递减区间观察下面图象：yx2346021-15y=cosx(xR)当x=时，函数值y取得最大值1；k2当x=时，函数值y取得最小值-1k2)0,2k对称中心（kx对称轴：观察下面图象：函数性质y=sinx(kz)∈y=cosx(kz)∈定义域值域最值及相应的x的集合周期性奇偶性单调性对称中心对称轴x∈Rx∈R[-1,1][-1,1]x=2kπ时ymax=1x=2kπ+π时ymin=-1周期为T=2π周期为T=2π奇函数偶函数在x[2kπ∈，2kπ+π]上都是增函数,在x[2kπ-π∈，2kπ]上都是减函数。(kπ,0)x=kπx=2kπ+时ymax=1x=2kπ-时ymin=-1π2π2在x[2kπ-,2kπ+]∈上都是增函数,在x[2kπ+∈，2kπ+]上都是减函数.π2π2π23π2(kπ+,0)π2x=kπ+π2。x、最小值分别是什么的集合，并说出最大值最小值时的自变量写出取最大值、最小值吗？如果有，请、下列函数有最大值、例3RxxyRxxy,2sin3)2(,1cos)1(大小：性，比较下列各组数的、利用三角函数的单调例4)417cos()528cos()2()10sin()18sin(1与与）（练习：P451、2、3练习：P455还有其他方法来比较吗？作单位圆用三角函数线方法：利用正余弦函数的的最大（小）值.]2,2[),321sin(5的单调递增区间、求函数例xxy].3,35[]2,2[),321sin(,0,.1251212434352,]2,2[,434352232122]22,22[sin,321的单调递增区间是即函数所以由于于是且可知由得由的单调递增区间是函数解：令xxykZkkkkxZkkxkkxkkkzyxz练习：P454、6答案：4>,>,>,>85,86kk、小结：作业：2（3）（4）、4、5。