高三数学 圆锥曲线中最值问题课件 新人教A版必修3 课件VIP免费

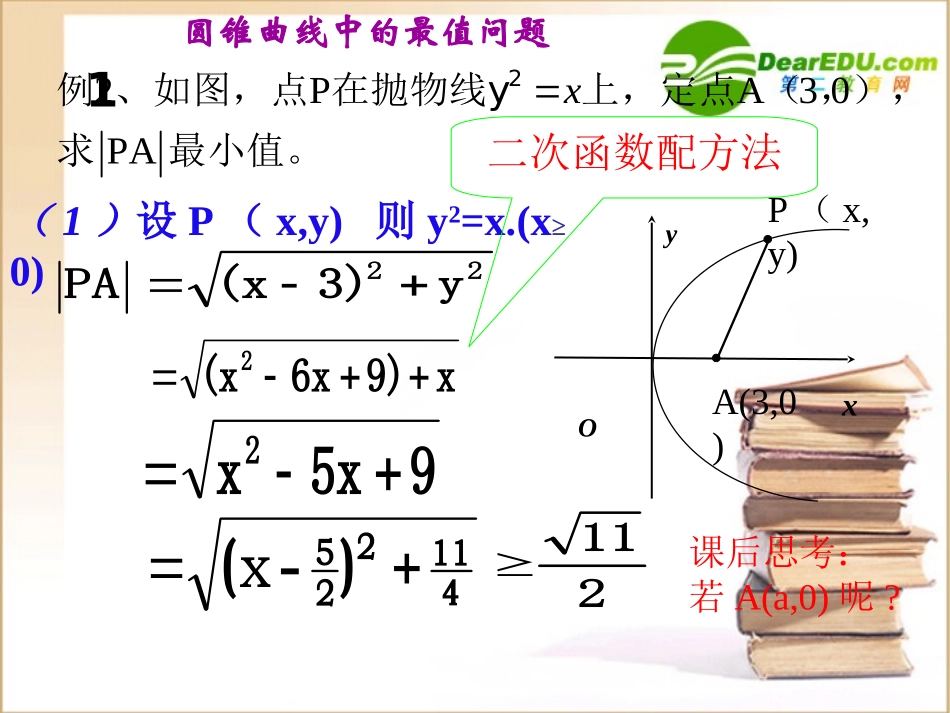
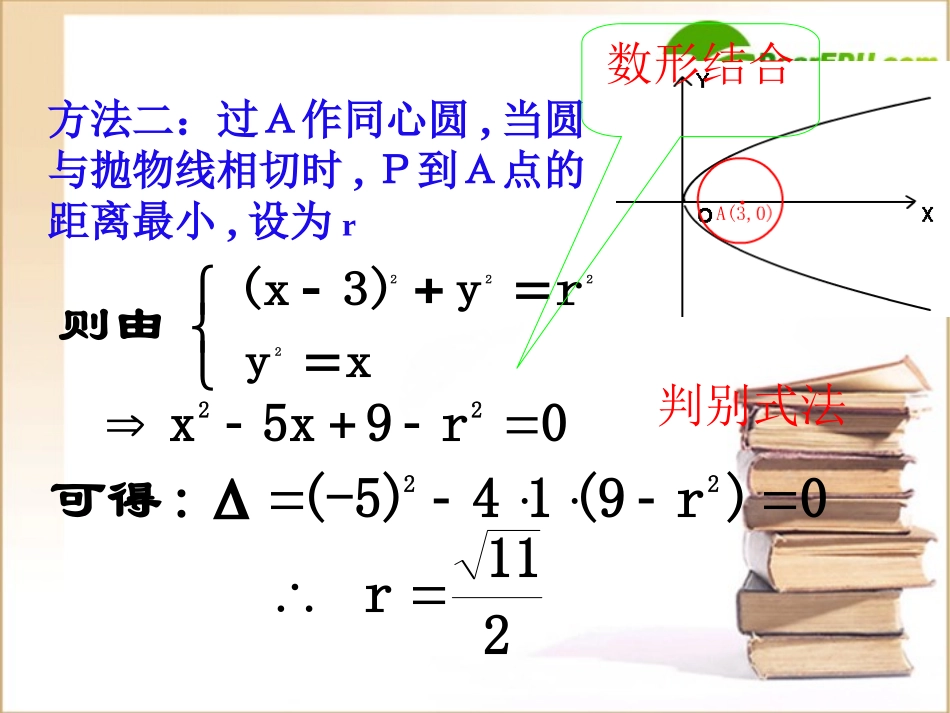
圆锥曲线中的最值问题2PA30PAx2例、如图，点在抛物线y上，定点（，），求最小值。（1）设P（x,y)则y2=x.(x≥0)y3)(xPA2295xx2x9)6x(x2411225)-(x211OyxP（x,y)A(3,0)二次函数配方法1课后思考：若A(a,0)呢?方法二：过Ａ作同心圆,当圆与抛物线相切时,Ｐ到Ａ点的距离最小,设为rxyry3)(x则由22220r95xx22211r0)r(914(-5)Δ:可得22数形结合判别式法变式若P为抛物线y2=x上一动点，Q为圆（x-3)2+y2=1上一动点，则|PQ|的最小值为__________1211点评：1）求曲线上一点到已知点的距离的最大（小）值，可过已知点作同心圆，当圆与曲线恰好相切时，则此公共点到已知点的距离最大（小）。2）求曲线上一动点到一已知圆上一动点的距离的最大（小）值问题，常转化为求曲线上的动点到圆心的距离的最大（小）值问题。OyxABP的最大值求PABS距离的最大值定直线到即求抛物线上一动点ABP圆锥曲线中的最值问题知识迁移变题例2：已知抛物线y2=4x，以抛物线上两点A(4,4)、B(1,-2)的连线为底边的△ABP，其顶点P在抛物线的弧AB上运动，求：△ABP的最大面积及此时点P的坐标。动点在弧AB上运动，可以设出点P的坐标，只要求出点P到线段AB所在直线AB的最大距离即为点P到线段AB的最大距离，也就求出了△ABP的最大面积。要使△ABP的面积最大，只要点P到直线AB的距离d最大。解：由已知：|AB|=22)24()14(2x-y-4=0直线AB：*解题过程如下：*分析：d=5425442yyyx528y2y25291y2）（由已知：－2＜y＜4∴dmax=529此时，y=1,x=41d21AB=2152953427∴点的坐标为(，1)41∴Smax=设P(x,y).y2=4x我们可以连接AB，作平行AB的直线L与抛物线相切，求出直线L的方程，即可求出直线L与AB间的距离，从而求出△ABP面积的最大值和点P的坐标。分析：y2-2y+2m=0设直线L与抛物线y2=4x相切，直线AB：2x-y-4=0直线L的方程为：2x-y+m=0（*）△=4-8m=0,m=21此时，y=1,x=41∴直线L的方程为：2x-y+=021两直线间的距离d=529另解：把（*）代入抛物线的方程得其他过程同上。cb222bac2c22ca22,1e2圆锥曲线中的最值问题221222124.190.xyFFPabFPFe例已知椭圆的焦点，，若在椭圆上存在一点使得，求离心率的取值范围1F2FxO),(yxPc,0c,0-mn3b不等式法还有其他的解法吗?•法二：设|PF1|=m,|PF2|=n,21PFF则cos=0242)(2422222mncmnnmmncnm0124422mnca22244)2(aanmmn22222244244acamnca01244222aca即0122e212e即22e当且仅当m=n时等号成立．22mine基本不等式)1,22[e点评：“不等式法”利用有关条件列出所求变量的不等关系式求解．例4.设M是椭圆13422yx上的动点，F是右焦点.定点A(1,1)求：１．MA+MF的最值２．MA+2MF的最小值分析：如图所示：xyMOFAF’M1M2M3M’A’1.由第一定义：MF+MF’=2a=4MF=4-MF’即求:4+(MA-MF’)最值dMFacdMF221d即求：MA+d的最小值2.由第二定义：解：1.设左焦点F’,由第一定义得：MA+MF=MA+2a-MF=4+(MA-MF’)55连结AF’延长交椭圆于M1，反向延长线交椭圆于M2则：M1,M2分别是MA-MF’取得最大和最小的点因为（MA-MF’）max=AF’=（MA-MF’）min=-所以（MA+MF）max＝４＋（MA+MF）min＝4-55因为椭圆的右准线L:x=4,设M在L上的射影为M’,由第二定义知：'221'MMMFacMMMF'2MMMAMFMA过A作AA’于L，交椭圆于M3，则：M3使MA+MM’达到最小的点所以（MA+2MF）min=4-1=3几何法点评：几何法适应于当条件和结论具有明显的几何特征及意义时，可考虑采用数形结合法，从几何特征下手来处理，利用圆锥曲线的性质如第一，二定义转化，和平面几何知识解决．求圆锥曲线最值问题的主要方法有哪些？1、函数法(建立目标函数)2、判别式法（转化为一元二次方程）4、几何法（借助图形的几何性质）3、不等式法(布列所求变量的不等式)小结1.掌握求圆锥曲线中的有关最值的基本方法：2.解析几何是研究“形”的科学，在求圆锥曲线的最值问题时要善于结合图形，通过数形结合将抽象的问题、繁杂的问题化归为动...