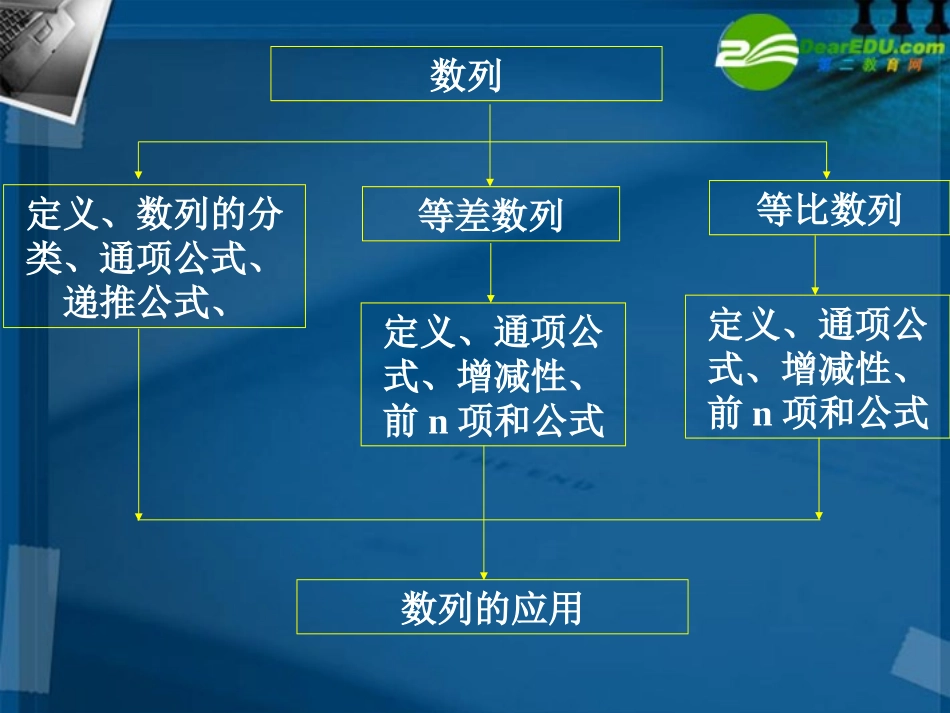
第二章数列数列定义、数列的分类、通项公式、递推公式、等差数列等比数列定义、通项公式、增减性、前n项和公式定义、通项公式、增减性、前n项和公式数列的应用(6)Sn与an的关系:1112,,nnnSnaSSn(5)数列的前n项和:Sn=a1+a2+a3+…+an一、知识要点数列等差数列等比数列定义an-an-1=d(n∈N*,且n≥2)an=qan-1(n∈N*,且n≥2)通项公式an=a1+(n-1)dan=a1qn-1前n项和公式或性质a1+an=a2+an-1=…;a1+a2n-1=2an;p+q=m+nap+aq=am+ana1an=a2an-1=…;a1a2n-1=(an)2;p+q=m+napaq=aman若{an}是等差数列,则Sn,,S2n-Sn,,S3n-S2n也是等差数列若{an}是等比数列,则Sn,,S2n-Sn,,S3n-S2n也是等比数列2)(1nnaanSdnnnaSn2)1(1一、知识要点11111111)()()nnnnaqSaaqaqqqq()nmnmaqanmaadnm一、知识要点121321=+()+()+()nnnaaaaaaaa…+3.数列的通项公式(2)公式法:等差数列、等比数列(3)叠加法:(4)累乘法:321121=nnnaaaaaaaa…(5)构造法:(1)观察法:1112,,nnnSnaSSn(1)公式法:等差数列、等比数列4.常见的求和方法(2)Sn法:(3)错位相减法:型如{anbn}的数列求和,其中{an}为等差数列,{bn}为等比数列.一、知识要点2323nnSxxxnx如:求(1)公式法:4.常见的求和方法(2)Sn法:(3)错位相减求和法:(4)裂项求和法:一、知识要点(5)分组求和法:12111(08)121(20).(1)(),(2)*{},,,(),{}.{}天津在数列中且设证明是等比数列求数列的通项公式nnnnnnnnnaaaaqaqanqbaanNba(3)若a3是a6与a9的等差中项,求q的值;并证明:对任意的n∈N*,an是an+3与an+6的等差中项.二、巩固练习