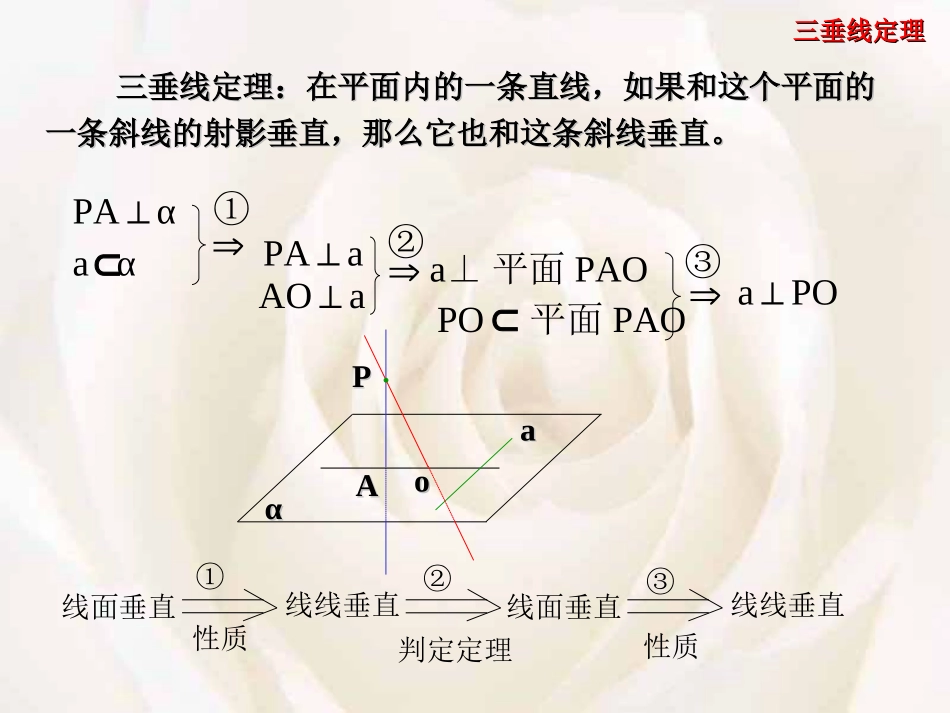
三垂线定理三垂线定理aaAAPPooαα复习:复习:什么叫平面的斜线、垂线、射影?什么叫平面的斜线、垂线、射影?如果如果aα,aAO⊥aα,aAO⊥,,思考思考aa与与POPO的位置关的位置关系如何?系如何?aaAAPPooααPOPO是平面是平面αα的斜线的斜线,,OO为斜足为斜足;;PAPA是平面是平面αα的垂线的垂线,A,A为垂足为垂足;;AOAO是是POPO在平面在平面αα内的射内的射影影..三垂线定理三垂线定理性质判定定理性质线面垂直①线线垂直②线面垂直③线线垂直PO平面PAOaPO⊥③三垂线定理:在平面内的一条直线,如果和这个平面的三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。一条斜线的射影垂直,那么它也和这条斜线垂直。PAα⊥aα①PAa⊥AOa⊥②a⊥平面PAO三垂线定理三垂线定理PPaaAAooαα直直a在一定要在平面内,如果a不在平面内,定理就不一定成立。PAOaα例如:当b⊥时,b⊥OA如果将定理“在平面内”的条件去掉,结论仍然成立吗?b但b不垂直于OP11、三垂线定理描述的是、三垂线定理描述的是PO(PO(斜线斜线))、、AOAO((射射影影))、、a(a(直线直线))之间的垂直关系。之间的垂直关系。22、、aa与与POPO可以相交,也可以异面。可以相交,也可以异面。33、三垂线定理的实质是平面的一条斜线和、三垂线定理的实质是平面的一条斜线和平面内的一条直线垂直的判定定理。平面内的一条直线垂直的判定定理。说明:说明:三垂线定理三垂线定理例1直接利用三垂线定理证明下列各题:(1)已知:PA⊥正方形ABCD所在平面,O为对角线BD的中点求证:PO⊥BD,PC⊥BD(3)已知:在正方体AC1中,求证:A1C⊥B1D1,A1C⊥BC1(2)已知:PA⊥平面PBC,PB=PC,M是BC的中点,求证:BC⊥AMADCBA1D1B1C1(1)(2)BPMCA(3)POABCD(1)PA⊥正方形ABCD所在平面,O为对角线BD的中点,求证:PO⊥BD,PC⊥BDPOABCD证明: ABCD为正方形O为BD的中点∴AO⊥BD同理,ACBD⊥AC是PC在ABCD上的射影∴PC⊥BDPO⊥BD∴AO是PO在平面ABCD上的射影∴PA⊥平面ABCD BD平面ABCD又PMCAB(2)已知:PA⊥平面PBC,PB=PC,M是BC的中点,求证:BC⊥AM证明:PMBC⊥∴BC⊥AM∴PM是AM在平面PBC上的射影∴PA⊥平面PBC PB=PCM是BC的中点 BC平面PBC又(3)在正方体AC1中,求证:A1C⊥BC1,A1C⊥B1D1 在正方体AC1中A1B1⊥面BCC1B1且BC1⊥B1C∴B1C是A1C在面BCC1B1上的射影CBA1B1C1ADD1证明:CBA1B1C1ADD1同理可证,A1C⊥B1D1由三垂线定理知A1C⊥BC1PMCABPAOaαA1C1CBB1OAαaP我们要学会从纷繁的已知条件中找出或者创造出符合三垂线定理的条件解题回顾三垂线定理解题的关键:找三垂!怎么找?一找直线和平面垂直二找平面的斜线在平面内的射影和平面内的一条直线垂直注意:由一垂、二垂直接得出第三垂并不是三垂都作为已知条件解题回顾PAOaα关于三垂线定理的应用,关键是找出平面关于三垂线定理的应用,关键是找出平面((基准面基准面))的垂线。的垂线。至于射影则是由垂足、斜足来确定的,因而是第二位的。至于射影则是由垂足、斜足来确定的,因而是第二位的。从三垂线定理的证明得到证明从三垂线定理的证明得到证明a⊥ba⊥b的一个程序:一垂、的一个程序:一垂、二射、三证。即二射、三证。即第一、找平面第一、找平面((基准面基准面))及平面垂线及平面垂线第二、找射影线,这时第二、找射影线,这时aa、、bb便成平面上的一条直线便成平面上的一条直线与与一条斜线。一条斜线。三垂线定理三垂线定理第三、证明射影线与直线第三、证明射影线与直线aa垂直,从而得出垂直,从而得出aa与与bb垂垂直。直。PAOaα直直直直直直直直直直直直直直②直直直直PAOaα①直直直直③直直直直PAOaα直线和平面垂直平面内的直线和平面一条斜线的射影垂直平面内的直线和平面的一条斜线垂直线射垂直线斜垂直PAOaαPAOaα平面内的一条直线和平面的一条斜线在平面内的射影垂直平面内的一条直线和平面的一条斜线垂直三垂线定理的逆定理??在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。PAOaα已知:PA,PO分别是平面的垂线和斜线,AO是PO在平面的射影,a,a⊥PO求证:a...