高中数学 322立体几何中的向量方法-距离的向量计算方法课件 新人教A版选修2-1 课件VIP免费

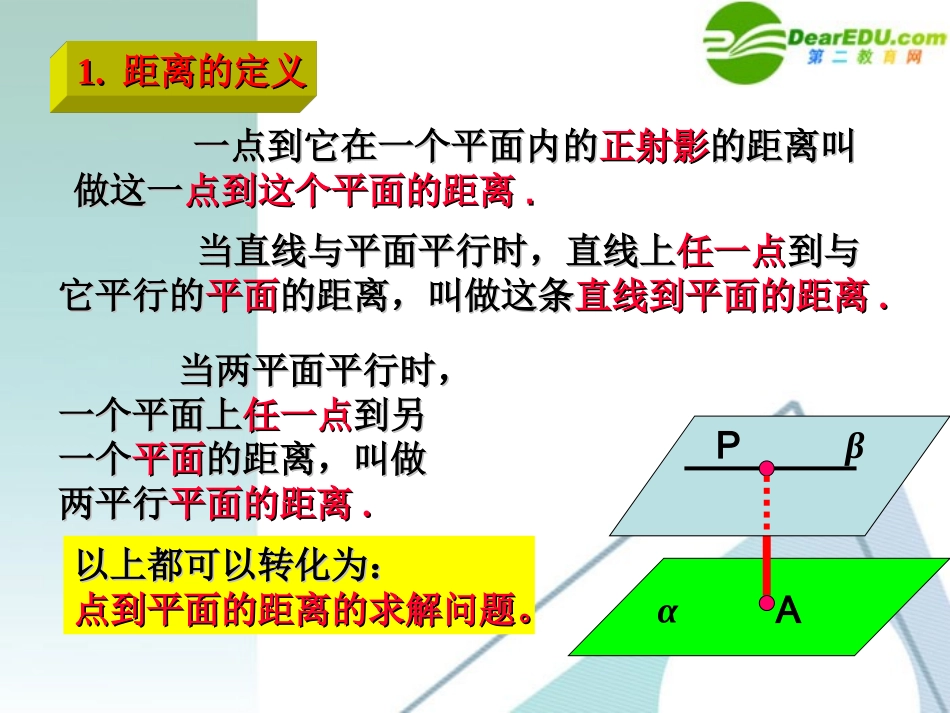
------距离的向量计算方法距离的向量计算方法Ctrl+Alt+M=菜单栏；Ctrl+Alt+T=工具栏；Ctrl+Alt+S=滚动条；Ctrl+Alt+H=窗口；Ctrl+Alt+B=背景（按一次组合键，显示，按同样的组合键，隐藏）αβ一点到它在一个平面内的一点到它在一个平面内的正射影正射影的距离叫的距离叫做这一做这一点到这个平面的距离点到这个平面的距离..PA1.1.距离的定义距离的定义当直线与平面平行时，当直线与平面平行时，直线上直线上任一点任一点到与到与它平行的它平行的平面平面的距离，叫做这条的距离，叫做这条直线到平面的距离直线到平面的距离..当两平面平行时，当两平面平行时，一个平面上一个平面上任一点任一点到另到另一个一个平面平面的距离，叫做的距离，叫做两平行两平行平面的距离平面的距离..以上都可以转化为：以上都可以转化为：点到平面的距离的求解问题。点到平面的距离的求解问题。如图A,空间一点P到平面的距离为d,已知平面的一个法向量为n,且AP�与n不共线,能否用AP�与n表示d?分析:过P作PO⊥于O,连结OA.则d=|PO�|=||cos.PAAPO� PO�⊥,,n∴PO�∥n.∴cos∠APO=|cos,PAn�|.∴d=|PA�||cos,PAn�|=|||||cos,|||PAnPAnn��=||||PAnn��.nAPO2.2.点到平面距离的向量计算公式点到平面距离的向量计算公式αβACB点B到平面α的距离:||ABndn�n是平面的法向量n这个结论说明,平面外一点到平面的距离等于连结此点与平面上的任一点(常选择一个特殊点)的向量在平面的法向量上的射影的绝对值.2.2.点到平面距离的向量计算公式点到平面距离的向量计算公式DDCCAABBGGEEFFyyzz(020FB�，，）如图建立空间坐标系，如图建立空间坐标系，(nxyz，，）G(0,4,2)G(0,4,2)E(2,0,0),E(2,0,0),F(4,2,0),F(4,2,0),00GEnGFn�，(422(242GFGE�，，）,，，）(113n，，）FBndn�(020FB�，，）11112 ∴∴24204220xyzxyz则则∴∴则则设平面的法向量设平面的法向量∴∴例例1.1.ABCDABCD是边长为是边长为44的正方形，的正方形，EE、、FF分别是分别是ADAD、、ABAB的中点，的中点，GCGC垂直平面垂直平面ABCDABCD，，GCGC＝＝22，求点，求点BB到平面到平面EFGEFG的距离的距离..解：解：xx3.3.点到平面的距离的向量计算示例点到平面的距离的向量计算示例练习(用向量法求距离):1.如图,ABCD是矩形,PD平面ABCD,PDDCa,2ADa,、MN分别是、ADPB的中点,求点A到平面MNC的距离.例例22则D(0,0,0),A(,0,0),B(,,0),C(0,,0),P(0,0,)2aa2aaa解：如图,以D为原点建立空间直角坐标系D－xyz. 、MN分别是、ADPB的中点,∴2(,0,0)2Ma211(,,)222Naaa∴2(,,0)2MCaa�,11(0,,)22MNaa�,2(,0,0)2MAa�设(,,)nxyz为平面MNC的一个法向量,∴,nMNnMC��3.3.点到平面的距离的向量计算示例点到平面的距离的向量计算示例练习(用向量法求距离):1.如图,ABCD是矩形,PD平面ABCD,PDDCa,2ADa,、MN分别是、ADPB的中点,求点A到平面MNC的距离.∴2(,,0)2MCaa�,11(0,,)22MNaa�,2(,0,0)2MAa�设(,,)nxyz为平面MNC的一个法向量,∴,nMNnMC��∴202nMCaxay��且022aanMNyz��解得22xyz,∴可取(2,1,1)m�∴MA�在n上的射影长2MAnadn�即点A到平面MNC的距离为2a.例例223.3.点到平面的距离的向量计算示例点到平面的距离的向量计算示例ABCDA1B1C1D1和两条异面直线都垂直相交的直线，我们称之为异面直线的公垂线.公垂线段的长度，叫做两条异面直线间的距离.两条异面直线的公垂线在这两条异面直线间的线段叫做公垂线段.异面直线,ab之间的距离：11||ACndAAn�(,,)annnb为方便，称为公垂向量nab4.4.两异面直线的距离定义及向量计算公式两异面直线的距离定义及向量计算公式例3已知正方体1AC的棱长为a，求1BC与BD间的距离奎屯王新敞新疆zyxB1A1C1BAD1DC解：如图建立空间直角坐标系，则1(,,0),(0,,0),(,,),(0,0,0)BaaCaBaaaD1(,,0),(,0,)DBaaCBaa�所以10(1,1,1)0nDBaxaynnCBaxaz...