高一数学函数的单调性 浙教版 课件VIP免费

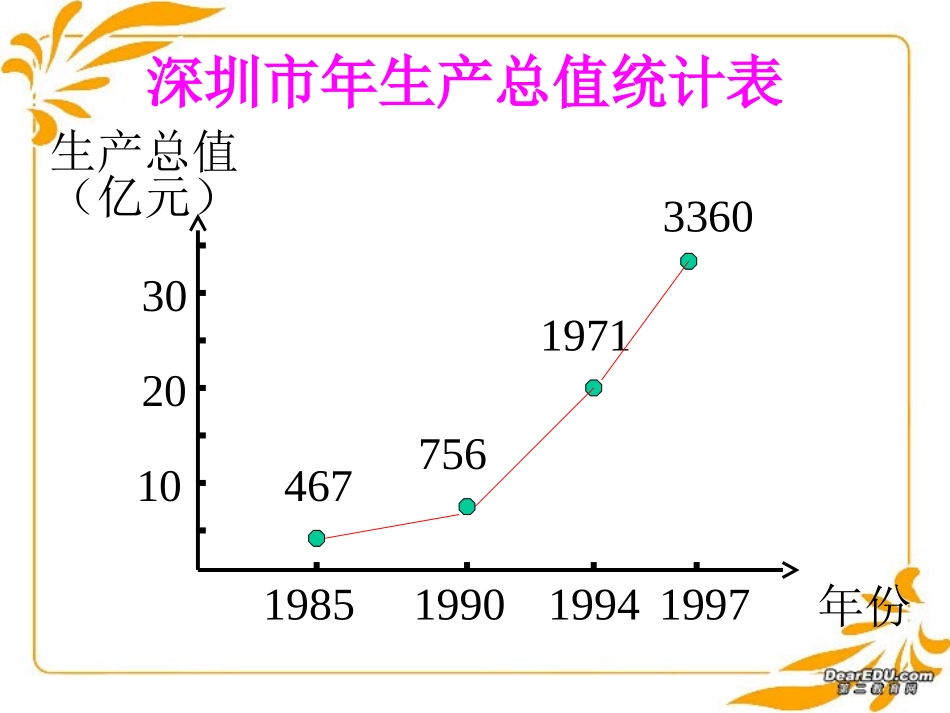
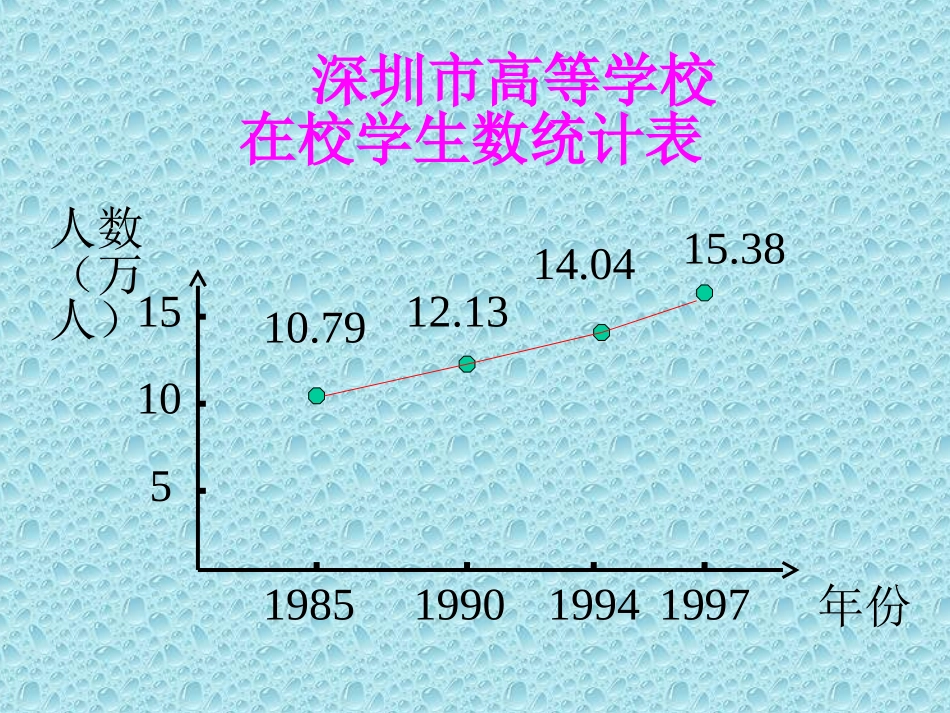
函数的单调性函数的单调性46775619713360深圳市年生产总值统计表19851990199419971020年份生产总值（亿元）3079.1013.1204.1438.15深圳市高等学校在校学生数统计表19851990199419971015年份人数（万人）5Oxy1xy11Oxy2x2y21Oxy2yx2yOxx1y,,21xx在给定区间上任取21xx)f(x)f(x21函数f(x)在给定区间上为增函数。Oxy)x(fy如何用x与f(x)来描述上升的图象？)x(f11x如何用x与f(x)来描述下降的图象？,,21xx在给定区间上任取21xx函数f(x)在给定区间上为减函数。)f(x)f(x21)x(f1)x(f2)x(fyOxy1x2x)x(f22x如果对于属于定义域I内的某个区间上的任意两个自变量的值x1、x2，当x1＜x2时，都有f（x1）＜f（x2），那么就说f（x）.在这个区间上是增函数.如果对于属于定义域I内的某个区间上的任意两个自变量的值x1、x2，当x1＜x2时，都有f（x1）>f（x2），那么就说f（x）.在这个区间上是减函数.增函数与减函数定义说明•函数y=f(x)在区间D上是增函数或减函数，就称函数y=f(x)在区间D上具有单调性，•D称为函数的单调区间。-5Oxy12345-1-2-3-4123-1-2例:下图是定义在[－5，5]上的函数y＝f（x）的图象，根据图象说出y＝f（x）的单调区间，以及在每一单调区间上，y＝f（x）是增函数还是减函数.解：y＝f（x）的单调区间有[－5，－2），[－2，1）[1，3），[3，5].其中y＝f（x）在[－5，－2），[1，3）上是减函数，在[－2，1），[3，5）上是增函数.作图是发现函数单调性的方法之一.单调递增区间：单调递减区间：]1,(),1[xx2x)x(f2y21o的单调区间判断函数xxxf2)(2）上是增函数。，（在区间证明函数1x2)x(f[例1]内任意是区间设),(x,x21)x2(x)1x2()1x2()x(f)x(f2121210xx,xx21210)x(f)x(f21)x(f)x(f21即),(1x2)x(f在区间则函数证明：。两个实数，且xx21是增函数。（条件）（论证结果）（结论）证明函数单调性的步骤•①设值：x1,x2∈Ｉ，且x1