高中数学 二元一次不等式与平面区域课件 新人教A版必修5 课件VIP免费

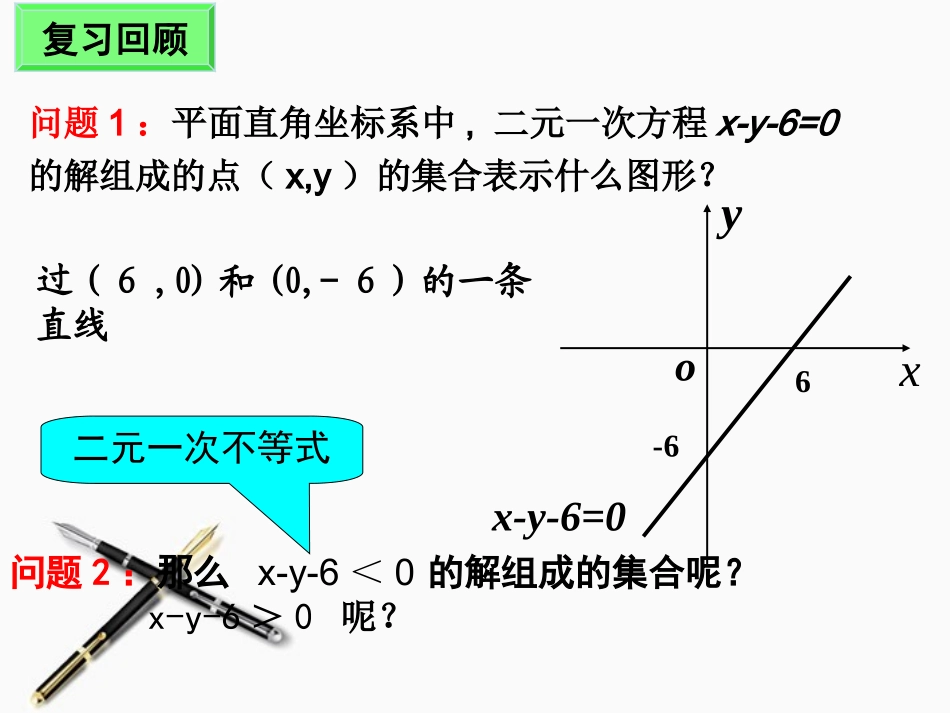
3.3.1二元一次不等式与平面区域问题1：平面直角坐标系中,二元一次方程x-y-6=0的解组成的点（x,y）的集合表示什么图形？复习回顾x-y-6=0xyo6-6过(６,0)和(0,-６)的一条直线问题2：那么x-y-6＜0的解组成的集合呢？x-y-6＞0呢？二元一次不等式（1）二元一次不等式：含有两个未知数，并且未知数的最高次数是1的不等式；（2）二元一次不等式的解集：所有满足二元一次不等式的有序实数对（x，y）构成的集合二元一次不等式的定义下面研究一个具体的二元一次不等式引例：x–y-6<0的解集所表示的图形。06yx问题3：平面直角坐标系内的点被直线分为哪三类？直线把平面内所有点分成三类:a)在直线x–y–6=0上的点c)在直线x–y–6=0右下方区域内的点b)在直线x–y–6=0左上方区域内的点Oxyx–y=6左上方区域右下方区域-66问题4：直线左上方的平面区域如何表示？右下方的平面区域呢？06yx请同学们画出直线x-y-6=0的图像几何画板实验一分别作出下列点的坐标并观察它们在坐标系中的位置,分组讨论：小组（1）小组（2）A(-3,0),B(3,3),C(6,6)D(3,-6),E(6,-3),F(9,0)几何画板实验二结论不等式x–y-6<0表示直线x–y=6左上方的平面区域；不等式x–y-6>0表示直线x–y=6右下方的平面区域；直线叫做这两个区域的边界。注意：把直线画成虚线以表示区域不包括边界归纳总结、揭示新知结论：一般地，二元一次不等式0CyAxB在平面直角坐标系中表示直线0CyAxB某一侧所有点组成的平面区域。总结：我们把直线画成虚线以表示区域不包含边界直线。画不等式0CyAxB所表示的平面区域时，此区域包括边界直线，应把边界直线画成实线。问题5：0CyAxB表示的平面区域与0CyAxB有何不同？如何体现这种区别？表示的平面区域问题6：直线0CyAxB同一侧所有的点（x，y）代入CyAxB所得实数符号如何？问题7：如何判断0CyAxB表示直线0CyAxB哪一侧平面区域？特殊点0CyAxB同一侧的所有点(x,y)，把坐标(x,y)代入CyAxB，所得到实数的符号都相同，所以只需要在直线的某一侧取一个(x0,y0)，从CAyx00B的正负即可判断不等式0CyAxB表示直线哪一侧的平面区域。一般把特殊点取为坐标原点，这种方法称为代点法.区域确定:)0,0(归纳总结:二元一次不等式Ax＋By＋C＞0表示的平面区域常用“直线定界，特殊点定域”的方法，即画线——取点——判断.归纳总结:例1：画出不等式x+4y<4表示的平面区域x+4y-4=0解：(1)直线定界:先画直线x+4y–4=0（画成虚线）所以，原点在x+4y–4<0表示的平面区域内，不等式x+4y–4<0表示的区域如图所示。典例剖析：(2)特殊点定域:取原点（0，0），代入x+4y-4，因为0+4×0–4=-4<0xyO41例2将下列图中的平面区域（阴影部分）用不等式出来（图（1）中的区域不包含y轴）xyox+y=0(2)yxo(1)解(1)x>0(2)x+y≥0yxo2x+y=4(3)(3)2x+y<4例题分析1.判断下列命题是否正确(1)点(0,0)在平面区域x+y≥0内;()(2)点(0,0)在平面区域x+y+1<0内;()(3)点(1,0)在平面区域y>2x内；()(4)点(0,1)在平面区域x-y+1>0内.()2.不等式x+4y-9≥0表示直线x+4y-9=0()A.右上方的平面区域B.右上方的平面区域(包括直线)C.左下方的平面区域D.左下方的平面区域(包括直线)感受理解×B√××小结和作业作业：P93A组1题小结：⑴二元一次不等式表示平面区域：直线某一侧所有点组成的平面区域。⑵判定方法：直线定界，特殊点定域。知识点数学思想1、数形结合2、由特殊到一般