高三数学离散型随机变量的方差课件 人教版 课件VIP免费

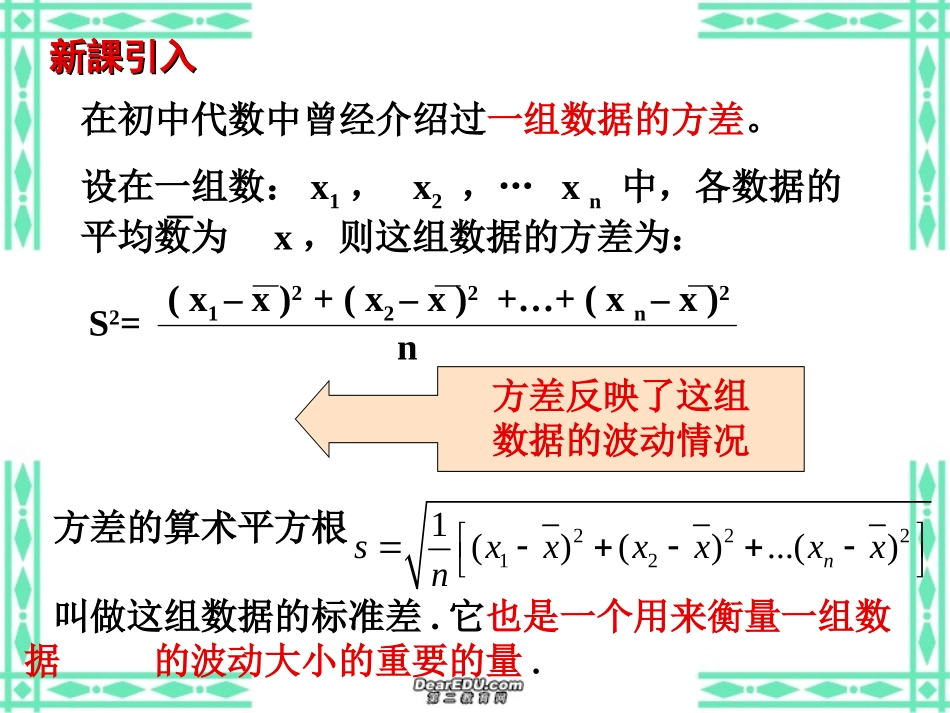
前課複習前課複習1、离散型随机变量ξ的期望Eξ=x1p1+x2p2+…xnpn+…2、满足线性关系的离散型随机变量的期望E（aξ+b)=aEξ+b3、服从二项分布的离散型随机变量的期望Eξ=np即若ξ~B（n,p),则4、服从几何分布的随机变量的期望若p(ξ=k)=g(k，p)，则Eξ=1/p新課引入新課引入在初中代数中曾经介绍过一组数据的方差。(x1–x)2+(x2–x)2+…+(xn–x)2nS2=设在一组数：x1，x2，…xn中，各数据的平均数为x，则这组数据的方差为：方差反映了这组数据的波动情况方差的算术平方根叫做这组数据的标准差.它也是一个用来衡量一组数据的波动大小的重要的量.222121()()...()nsxxxxxxn新課教學新課教學1、离散型随机变量的方差若离散型随机变量的分布列为ξPx1P1P2x2xnPn…………Dξ=（x1-Eξ)2·P1+（x2-Eξ)2·P2+…+（xn-Eξ)2·Pn+…叫随机变量ξ的均方差，简称方差。②、标准差与随机变量的单位相同；③、随机变量的方差与标准差都反映了随机变量取值的稳定与波动，集中与分散的程度。①、Dξ的算术平方根√Dξ——随机变量ξ的标准差，记作σξ；注意：2、满足线性关系的离散型随机变量的方差若η=aξ+b，则η的分布列为ηPP1P2ax2+bPn…………ax1+baxn+bDη=[ax1+b-E(aξ+b)]2·P1+[ax2+b-E(aξ+b)]2·P2+…+[axn+b-E(aξ+b)]2·Pn+…D（aξ+b）=a2·Dξ3、服从二项分布的随机变量的方差设ξ~B（n,p），则Dξ=qEξ=npq，q=1-p4、服从几何分布的随机变量的方差若p(ξ=k)=g(k，p)，则Eξ=1/p2pqDξ123…k…Pppqpq2…pqk-1…1、已知随机变量的分布列为-101P213161=3+1E=，D=.E=，D=.3195385例题讲解例题讲解2、若随机变量服从二项分布，且E=6，D=4,则此二项分布是。设二项分布为~B(n,p),则E=np=6D=np(1-p)=4n=18p=1/3实例应用实例应用例1：已知离散型随机变量ξ1的概率分布离散型随机变量ξ2的概率分布求这两个随机变量的期望、方差与标准差。ξ1P12345671/71/71/71/71/71/71/7ξ1P3.73.83.944.14.24.31/71/71/71/71/71/71/7说明：Eξ1=Eξ2，但Dξ1>Dξ2反映了ξ2比ξ1稳定，波动小。例2：甲乙两人每天产量相同，他们每日生产的次品个数分别为，其分布列为0123P0.30.30.20.2012P0.10.50.4判断甲乙两人生产水平的高低？实例应用实例应用E=0×0.3+1×0.3＋2×0.2＋3×0.2=1.3E=0×0.1+1×0.5＋2×0.4=1.3D=(0－1.3)2×0.3+(1－1.3)2×0.3＋（2－1.3）2×0.2＋（3-1.3)2×0.2=1.21D=(0－1.3)2×0.1+(1－1.3)2×0.5＋（2－1.3）2×0.4=0.4甲乙两人次品个数的平均值相等，但甲的稳定性不如乙，乙的生产水平高。期望值高，平均值大，水平高。方差值小，稳定性高，水平高练习1：若随机变量的概率分布满足P(=1)=p,P(=0)=1－p求DE=，D=.01PP1-PpP(1-p)課堂練習課堂練習課堂練習課堂練習課堂練習課堂練習課堂練習課堂練習課堂練習課堂練習课堂小结课堂小结1、离散型随机变量的方差Dξ=（x1-Eξ)2·P1+（x2-Eξ)2·P2+…+（xn-Eξ)2·Pn+…2、满足线性关系的离散型随机变量的方差D（aξ+b）=a2·Dξ3、服从二项分布的随机变量的方差Dξ=qEξ=npq，（q=1-p）4、服从几何分布的随机变量的方差2pqD