辽宁省沈阳二中高三数学必修5课件：正弦定理(1)(2) 课件VIP免费

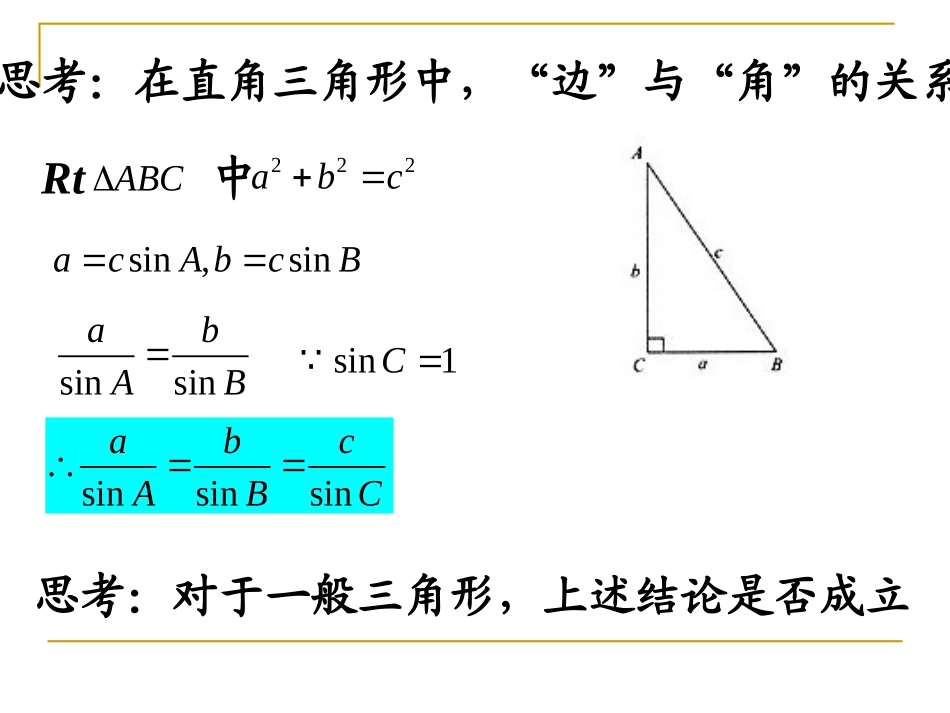
正弦定理和余弦定理正弦定理和余弦定理沈阳二中数学组沈阳二中数学组高中数学⑤B版1.1.11.1.1正弦定理正弦定理第一节思考：在直角三角形中，“边”与“角”的关系Rt中ABC222abcsin,sinacAbcBsinsinabABsin1CsinsinsinabcABC思考：对于一般三角形，上述结论是否成立在锐角三角形中，CDABD作于点sin,sinCDACDbAb即sin,sinCDBCDaBa即sinsinbAaBsinsinabAB即sinsinacAC同理：sinsinsinabcABC在钝角三角形中，CDABABD作交的延长线于点sin,sinCDACDbAb即sin180sin,sinCDBBCDaBa即sinsinbAaBsinsinabAB即sinsinacAC同理：sinsinsinabcABC由以上三种情况的讨论可得：正弦定理：sinsinsinabcABC思考：用“向量”的方法如何证明“正弦定理”在一个三角形中，各边的长和它所对角的正弦的比相等，即iAB�向量是与向量垂直的单位向量iABBCiAC�iBCiAC�coscoscoscos2222aBbAaBbA或sinsinabAB即sinsinaBbAsinsinacAC同理：sinsinsinabcABC思考：用“三角形面积公式”如何证明“正弦定理”∵BACDabcaABCahS21而CbBcADhasinsin∴CabBacSABCsin21sin21同理∴BacAbcCabSABCsin21sin21sin21haAbcSABCsin212sinsinsinABCabcabcSABC例、已知，根据下列条件，求相应的三角形中其它边和角的大小（保留根号或精确到0.1）ABC160,45,10;ABa23,4,30;abA35,2,120;abB436,6,120;bcB10675,8.2,11.2;3Cbc41.8,108.8,5.7;BCc138.2,11.8,1.2;BCc或无解45,15,2.2;CAa三角形的元素：三角形的三个角和它的对边解三角形：已知三角形的几个元素求其他元素的过程ABCAADBCDBDABDCAC例、在中，的平分线与边相交于点，求证：ABDCAD证明：在和中，由正弦定理得：,sinsinBDAB①,sinsinsin180DCACAC②①÷②得：BDABDCAC（2R为△ABC外接圆直径）2sinsinsinabcRABC求证：证明：OC/cbaCBARCcRcCCCCCBA2sin2sinsin,90''2,2sinsinabRRAB同理'',,OBBCAC作外接圆过作直径连2sinsinsinabcRABC10,45,30,,ABCcACabB中，求和105,102,5652;BabCAacBbABC,,1,60,30和求中，30,90,2CAa练习：1.1.11.1.1正弦定理正弦定理第二节思考：正弦定理可以解哪些类问题①已知两角和任一边，求其他两边及一角。②已知两边和其中一边对角，求另一边的对角。（有唯一解）（何时有一解，二解，无解)sin,ABCAA(1)在中，由的值讨论有两个角或一个角，所以解不唯一。(2)已知a、b及A作三角形，其解的情况如下：①A为锐角时②A为直角或钝角时ACabab一解15,4,120abA，求B；判断解的个数：ABC25,4,90abA，求B；10335,,903abA，求B；420,28,40abA，求B；一解一解一解两解35sincos,513sin.ABCABC在中，已知，求.6563)sin(sin.54cos,sinsinsinsin,53sin.1312sin),,0(,135cosBACAABAbaBbAaBAABBB只能为锐角，可知由正弦定理又解：412cos,sin,sin.513ABCABC变式：在中，已知求.65336563sin.6533)sin(sin135cos)2(.6563)sin(sin135cos)1(.135cos,sinsin,1312sin53sin),0(,54cos或时，时，角，可以为锐角也可以为钝又解：CBACBBACBBBBAbaBABAAA221().4ABCSbcABC已知的面积，试确定的形状.20sin10)sin1(21,0)(410)sin1(21)(41sin21)(412222为等腰直角三角形且解：ABCcbAAcbAbccbAbccbAbccbS,,,,2cos(60).ABCABCabcbcaCA在中，设所对的边分别为，若，求sinsin2sin(cos60cossin60sin)sinsin()sincoscossinsinsincos3sincos(3sincos)sinsin1sin03sincos1sin(30).2303021030150120.BCACCBACACACCACACAACCCAAAAAA解：由正弦定理得即又