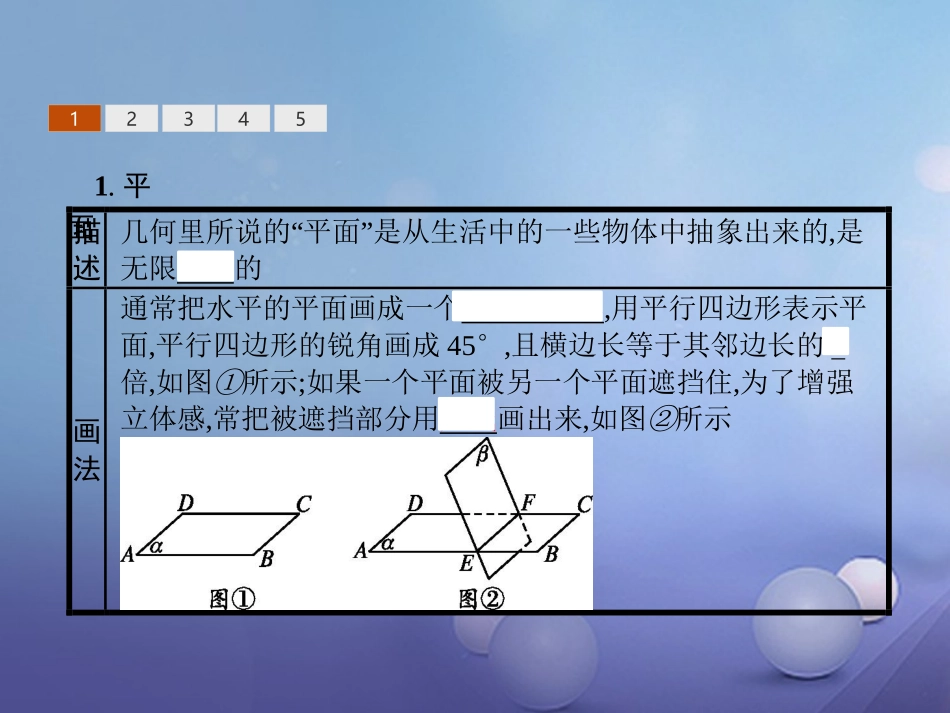
2.1.1平面1.知道平面的概念,了解平面的基本性质,会用图形和字母表示平面.2.能用符号语言描述空间中的点、直线、平面之间的位置关系.3.能用图形、文字、符号三种语言描述三个公理,理解三个公理的地位与作用,并能确定平面的个数.123451.平面描述几何里所说的“平面”是从生活中的一些物体中抽象出来的,是无限延展的画法通常把水平的平面画成一个平行四边形,用平行四边形表示平面,平行四边形的锐角画成45°,且横边长等于其邻边长的2倍,如图①所示;如果一个平面被另一个平面遮挡住,为了增强立体感,常把被遮挡部分用虚线画出来,如图②所示记法(1)用一个希腊字母α,β,γ等来表示平面,如上图①中的平面记为平面α(2)用两个大写的英文字母(表示平面的平行四边形相对的两个顶点)来表示平面,如上图①中的平面记为平面AC或平面BD(3)用四个大写的英文字母(表示平面的平行四边形的顶点)来表示平面,如上图①中的平面可记为平面ABCD1234512345【做一做1】如图所示的平行四边形MNPQ表示的平面不能记为()A.平面MNB.平面NQC.平面αD.平面MNPQ解析:MN是平行四边形MNPQ的一条边,不是对角线,所以该平面不能记作平面MN.答案:A123452.点、线、面的位置关系的表示A是点,l,m是直线,α,β是平面.文字语言符号语言图形语言点A在l上A∈l点A在l外A∉l点A在α内A∈α点A在α外A∉αl在α内l⊂α12345文字语言符号语言图形语言l在α外l⊄α或l,m相交于点Al∩m=Al,α相交于点Al∩α=Aα,β相交于lα∩β=l12345名师点拨从集合的角度理解点、线、面之间的关系(1)直线可以看成无数个点组成的集合,故点与直线的关系是元素与集合的关系,用“∈”或“∉”表示;(2)平面也可以看成点集,故点与平面的关系也是元素与集合的关系,用“∈”或“∉”表示;(3)直线和平面都是点集,它们之间的关系可看成集合与集合的关系,故用“⊂”或“⊄”表示.12345【做一做2-1】若点M在直线a上,a在平面α内,则M,a,α之间的关系可记为()A.M∈a,a∈αB.M∈a,a⊂αC.M⊂a,a⊂αD.M⊂a,a∈α答案:B12345【做一做2-2】若平面α与平面β相交于直线m,则用符号语言可表示为.答案:α∩β=m123453.公理1文字语言如果一条直线上的两点在一个平面内,那么这条直线在此平面内图形语言符号语言A∈l,B∈l,且A∈α,B∈α⇒l⊂α作用(1)判断点在平面内(2)判断直线在平面内(3)用直线检验平面12345名师点拨公理1的内容反映了直线与平面的位置关系.“线上两点在平面内”是公理的条件,结论是“线上所有点都在平面内”.从集合的角度看,这个公理就是说,如果一条直线(点集)中有两个点(元素)属于一个平面(点集),那么这条直线就是这个平面的真子集.12345【做一做3】已知直线m⊂平面α,点P∉m,点Q∈m,则()A.P∉α,Q∈αB.P∈α,Q∉αC.P∉α,Q∉αD.Q∈α解析:因为Q∈m,m⊂α,所以Q∈α.因为P∉m,所以有可能P∈α,也有可能P∉α.答案:D123454.公理2文字语言过不在一条直线上的三点,有且只有一个平面图形语言符号语言A,B,C三点不共线⇒有且只有一个平面α,使A∈α,B∈α,C∈α作用(1)确定平面(2)证明点共面12345名师点拨1.公理2的条件是“过不在一条直线上的三点”,结论是“有且只有一个平面”.2.公理2中“有且只有一个”的含义要准确理解.这里的“有”是说图形存在,“只有一个”是说图形唯一,强调的是存在和唯一两个方面,因此“有且只有一个”必须完整地使用,不能仅用“只有一个”来代替,否则就没有表达出存在性.12345【做一做4】三点可确定平面的个数是()A.0B.1C.2D.1或无数个解析:当这三点共线时,可确定无数个平面;当这三点不共线时,可确定一个平面.答案:D123455.公理3文字语言如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线图形语言符号语言P∈α,且P∈β⇒α∩β=l,且P∈l作用(1)判定平面相交(2)证明点共线(3)证明线共点12345【做一做5】如果两个平面有一个公共点,那么这两个平面()A.没有其他公共点B.仅有三个公共点C.仅有两个公共点D.有无数个公共点答案:D1231.对平面的理解剖析:几何中的平面是一个只描述而不定义的最基本的原始概念.生活中的平面是比较平整、有限的;而几何中所说的平面是从生活中常见的物体中抽象、概括出来的,是理想的、绝...