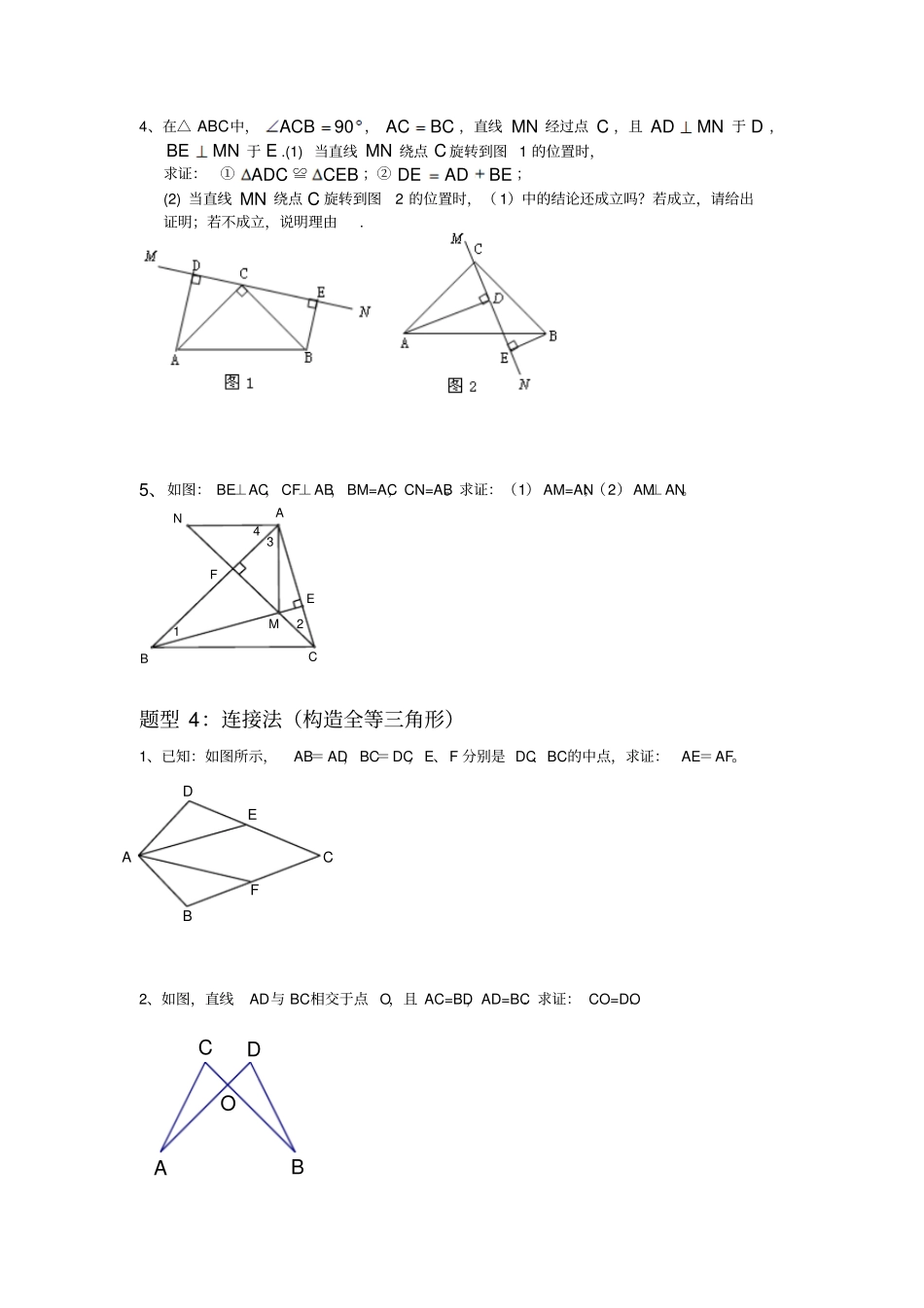
《全等三角形》证明题题型归类训练题型1:全等+等腰性质1、如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.求证:(1)△ABC≌△AED;(2)OB=OE.2、已知:如图,B、E、F、C四点在同一条直线上,AB=DC,BE=CF,∠B=∠C.求证:OA=OD.题型2:两次全等1、AB=AC,DB=DC,F是AD的延长线上的一点。求证:BF=CFFDCBA2、已知如图,E、F在BD上,且AB=CD,BF=DE,AE=CF,求证:AC与BD互相平分OCEBDAABEOFDC3、如图,在四边形ABCD中,AD∥BC,∠ABC=90°DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC.求证:BG=FG题型3:直角三角形全等(余角性质)1、如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.求证:BD=CG.2、如图,将等腰直角三角形ABC的直角顶点置于直线l上,且过A,B两点分别作直线的垂线,垂足分别为D,E,请你在图中找出一对全等三角形,并写出证明它们全等的过程.3、如图,∠ABC=90°,AB=BC,D为AC上一点,分别过A、C作BD的垂线,垂足分别为E、F求证:EF=CF-AEAFCBDEGABCFDE4、在△ABC中,90ACB,BCAC,直线MN经过点C,且MNAD于D,MNBE于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①ADC≌CEB;②BEADDE;(2)当直线MN绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.5、如图:BE⊥AC,CF⊥AB,BM=AC,CN=AB。求证:(1)AM=AN;(2)AM⊥AN。FBCAMNE1234题型4:连接法(构造全等三角形)1、已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:AE=AF。2、如图,直线AD与BC相交于点O,且AC=BD,AD=BC.求证:CO=DO.AODCBDBCAFE3、如图11-30,已知AB=AE,∠B=∠E,BC=ED,点F是CD的中点.求证:AF⊥CD.FEDCBA4、在正ABC内取一点D,使DADB,在ABC外取一点E,使DBEDBC,且BEBA,求BED.5、如图所示,BD=DC,DE⊥BC,交∠BAC的平分线于E,EM⊥AB,EN⊥AC,求证:BM=CN6、如图,在△ABD和△ACD中,AB=AC,∠B=∠C.求证:△ABD≌△ACD.ADCBACNEMBDDECBA题型5:全等+角平分线性质1、如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,且DB=DC,求证:EB=FC2、已知:如图所示,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,判断PM与PN的关系.题型6:倍长中线(线段)造全等前言:要求证的两条线段AC、BF不在两个全等的三角形中,因此证AC=BF困难,考虑能否通过辅助线把AC、BF转化到同一个三角形中,由AD是中线,常采用中线倍长法,故延长AD到G,使DG=AD,连BG,再通过全等三角形和等线段代换即可证出。1、已知:如图,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF,求证:AC=BFABCDEF2、已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EFFEDABC3、已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________.PDACBMNDCBA4、在△ABC中,AC=5,中线AD=7,则AB边的取值范围是()A、1