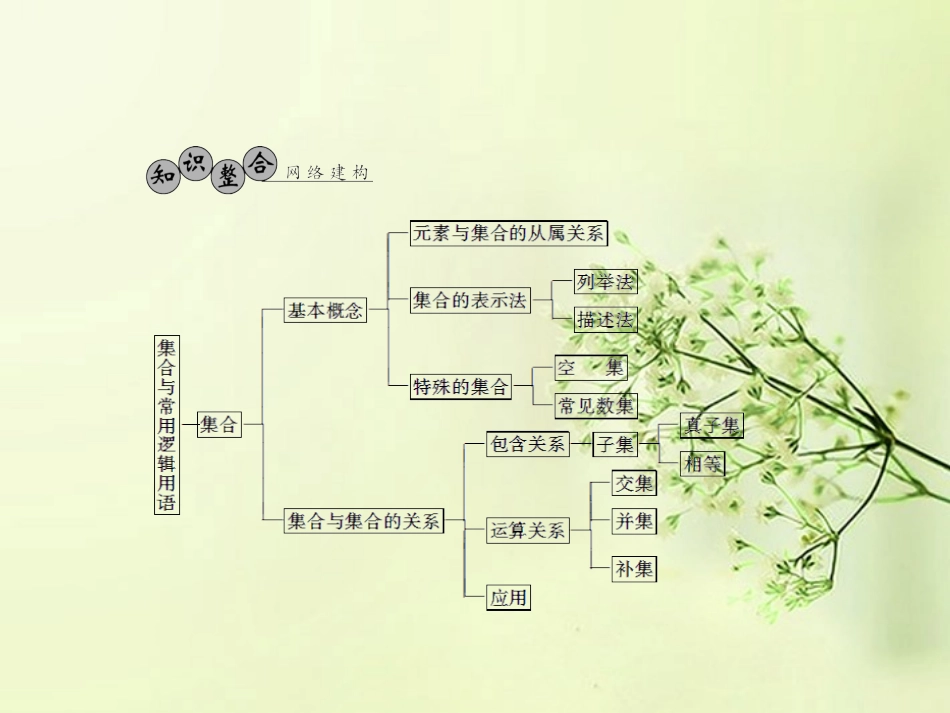
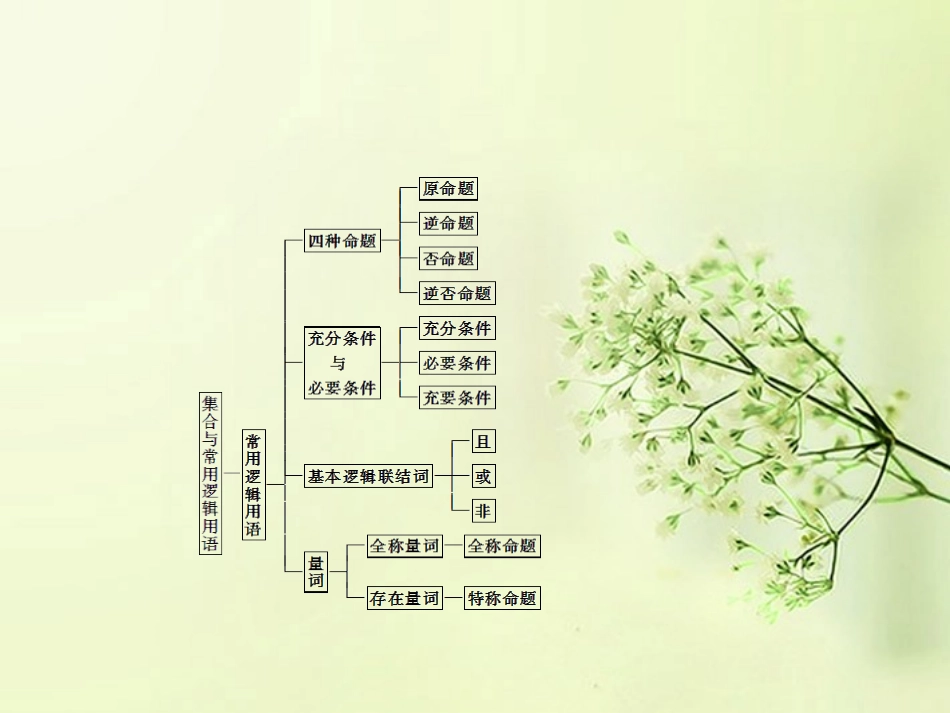
章末整合反馈遗忘空集的存在性也是常见的致误原因,在A⊆B、A∪B=B、A∩B=A、A∩B=∅中容易忽视集合A=∅这一情况,预防出现错误的方法是要注意分类讨论.已知集合A={x|x2-5x+4≤0},B={x|x2-2ax+a+2≤0},若A∩B=B,求实数a的取值范围.误区一漏掉特殊的子集空间【错解】A={x|1≤x≤4}∵A∩B=B,∴B⊆A令f(x)=x2-2ax+a+2∵B⊆A∴f(x)=0的两根在[1,4]内如图得:∴Δ≥01≤a≤4f1≥0f4≥0⇒2≤a≤187,综上所述:a∈2,187.【错解分析】错解是因为没有对集合B的元素认真分析,若B≠∅则上述解法正确;若B=∅呢?显然应补上B=∅时,a的范围,解法才完整.【正解】①B≠∅时.(同错解)②B=∅时,Δ=(-2a)2-4(a+2)=4a2-4a-8<0解得:-1<a<2,此时满足A∩B=B.综上可得:a的取值范围为-1,187.求解含参数的方程,不等式问题时,参数的不同取值,会产生不同的结果,解题时往往忽视对参数的讨论,从而导致解题错误.在R上函数f(x)=ax2+bx+c的值恒为正值的充要条件是什么?误区二忽略对参数的讨论【错解】f(x)=ax2+bx+c的值恒为正值的充要条件是a>0,Δ=b2-4ac<0.【错解分析】错解中没有考虑a=0的情况,若a=0时,在R上f(x)值恒为正数的充要条件是c>0,b=0.【正解】在R上f(x)的值恒为正数的充要条件是a>0b2-4ac<0或a=0c>0b=0.“否命题”与“命题的否定”不是同一个概念.“否命题”是对“原命题”的条件和结论同时进行否定;“命题的否定”只是对“原命题”的结论进行否定.写出“若x∈(A∩B)则x∈A且x∈B”的否定及否命题.误区三对命题的否定和否命题分辨不清造成错误【错解】否定:若x∉(A∩B)则x∉A且x∉B.否命题:若x∉(A∩B)则x∈A且x∈B.【错解分析】命题的否定是将命题的结论否定,而否命题是将条件和结论同时否定.【正解】否定:“若x∈(A∩B)则x∉A或x∉B”否命题:“若x∉(A∩B)则x∉A或x∉B”.含有量词命题的否定,除了把命题的结论否定外,还要注意量词的改变,即全称量词改为存在量词,存在量词改为全称量词.写出下列命题的否定形式:(1)矩形的四个角都是直角;(2)4<3.误区四全(特)称命题的否定形式错误【错解】(1)有的矩形四个角都不是直角.(2)4>3.【错解分析】(1)错误原因在于误认为“四个角都是直角”的否定为“四个角都不是直角”.而应有以下四种情况:①四个角都不是直角;②三个角不是直角;③二个角不是直角;④一个角不是直角.(2)忽略4=3的情况.【正解】(1)有的矩形四个角不都是直角.(2)4≥3.