湖南省株洲市四中高一函数的单调性 人教版 课件VIP免费

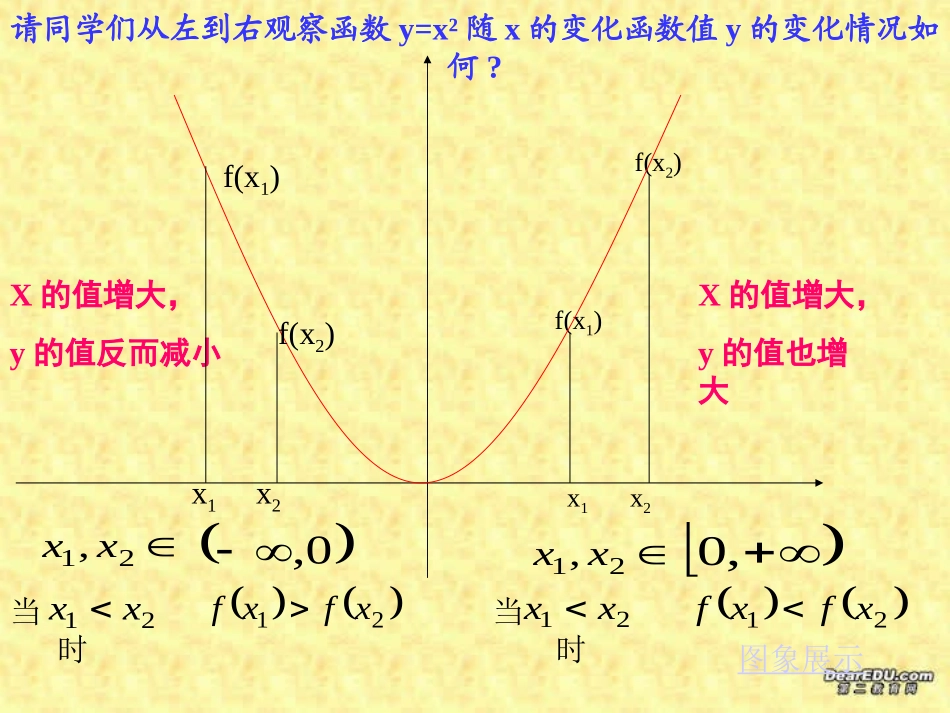
株洲市四中邓琼请同学们从左到右观察函数y=x²随x的变化函数值y的变化情况如何?f(x2)f(x1)x1x2X的值增大，y的值也增大X的值增大，y的值反而减小图象展示0,,021,xx21xfxf21xx当时21,xx当时21xx21xfxff(x1)f(x2)x1x2函数单调性的定义设函数的定义域为,如果对于属于内的某一个区间上的任意两个自变量的值当时，都有那么就说在这个区间上是增函数xfII2,1xx21xx21xfxfxfxfyxfyxfy21xfxff(x1)x1x2f(x2)f(x1)f(x2)x1x2减函数若函数在某个区间上是增函数或减函数，就说函数在这个区间具有严格的单调性，这个区间叫做的单调区间。判断函数y=x³的单调性f(x2)f(x1)x1x2y=x³整个图象随x值的增大y值也在增大Rxx21,时当21xx21xfxf增函数03xy0xy由图象法找出函数y=f(x)的单调区间并比较与的大小-5-2-10135[-5,-2)[-2,1)[1,3)[3,5]2f3f函数单调性定义要点：（1）函数的单调性又叫函数的增减性。（2）函数的单调性是对某个区间而言，是一个局部概念。也就是说，函数在定义域上可有几个单调区间（如：y=x²)（3）任意取由判断与的大小（4）增函数的图象是上升的，减函数的图象是下降的21,xxba,21xx1xf2xf证明：设是上的任意两个实数，且由得又由得于是即所以，在上是21,xx,021xx2112212111xxxxxxxfxf,0,21xx021xx21xx012xx021xfxf21xfxfxxf1,0判断函数在上的单调性，并证明结论xxf1,0减函数用定义法证明函数在某个区间上的单调性的方法步骤：（1）设给定区间，且（2）计算（往往通过因式分解、作差作积）至最简（3）判断上述差的符号（4）下结论（若差〈0，则为增函数，若差〉0，则为减函数）21,xx21xx21xfxf设点计算（作差变形）定号判断想一想：例2中（1）如果，函数是增函数还是减函数？课堂练习：判断函数在的单调性。0,xxxf1xxxf1)1,0(改成,0小结1、函数单调性是研究函数值y随自变量x的变化规律。2、判断函数单调性的方法：图象法定义法3、证明函数单调性的步骤（设点计算定号判断）拓展与思考（1）判断函数在上的单调性（2）证明函数在上是减函数作业：P6041,0xf13xxf,xx1