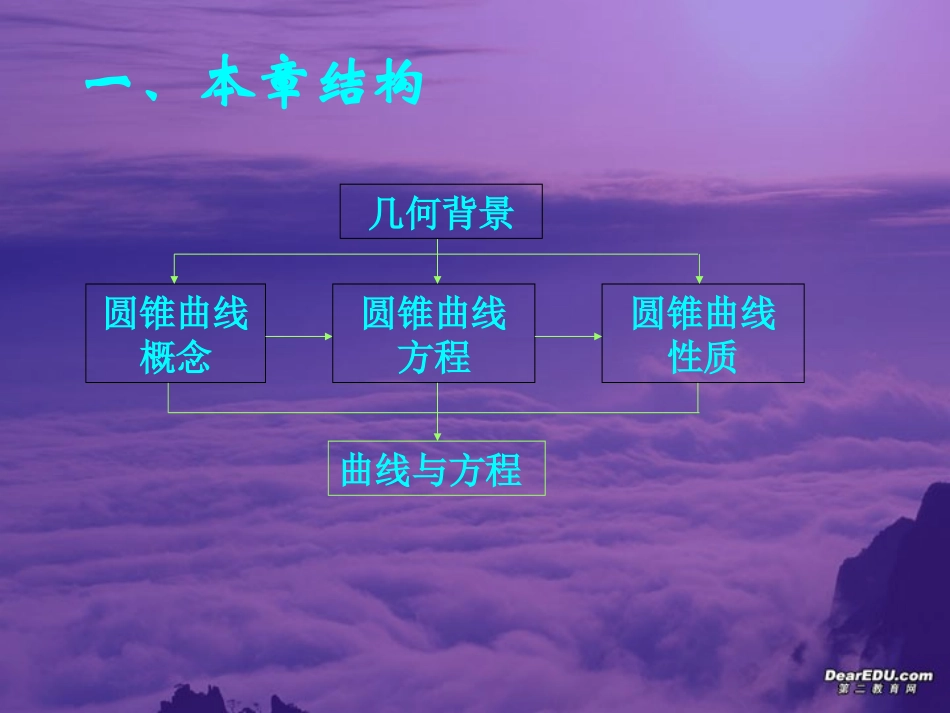
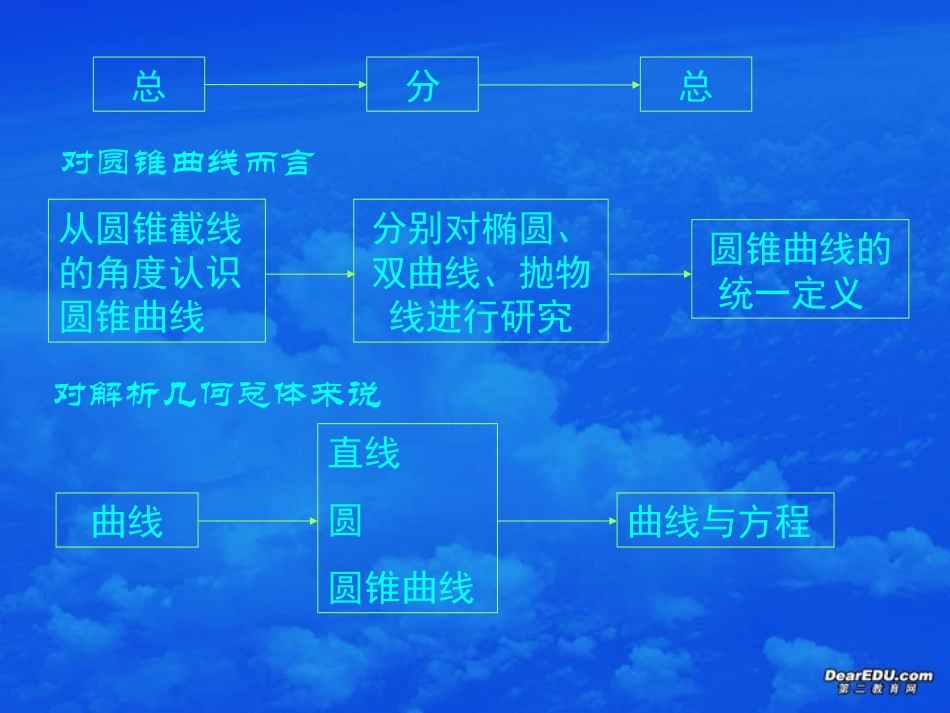
姜堰市第二中学一、本章结构圆锥曲线概念圆锥曲线方程圆锥曲线性质几何背景曲线与方程总分总从圆锥截线的角度认识圆锥曲线分别对椭圆、双曲线、抛物线进行研究圆锥曲线的统一定义对圆锥曲线而言对解析几何总体来说曲线直线圆圆锥曲线曲线与方程从统一的结构体现解析几何的基本思想几何特征建立方程研究性质二、教材分析与教学建议1。圆锥曲线的概念观察探索发现形成过程建议:(1)“适度引导”(2)重点在椭圆,另两个可直接给出(3)要求恰当,不要过分2。椭圆的标准方程(1)节首语:提出本节课题;本节课即解决其中的第一个问题;有些问题的解决贯穿全书,如光学性质。(2)给出了确定曲线类型的新方法(原方法:概念):曲线方程,这一点在必修部分已有体现,但未充分说明(3)突出建立椭圆方程的全过程:建系----立式----建立方程----简化方程P27第3、4行的一段话的说明(4)参数b的引入这里只需说明:简化方程形式,在后面应说明其几何意义(5)对焦点在y轴上的情形,可由学生独立研究不妨先作猜想3。椭圆的几何性质(1)要突出“用代数方法(方程)研究几何问题”的解析几何的基本思想如:范围、对称性等(2)对“顶点”,要说明“椭圆与对称轴的焦点”,不能认为最高(低)点、最左(右)点就是顶点(3)对离心率要突出其几何意义,并在实验的过程中感受和理解其意义。直观上椭圆的扁圆程度可用b/a来刻画,为什么用c/a呢?(4)用解析法研究曲线的几何性质是通过方程进行讨论的,而曲线方程又与所选择的坐标系有关,但不管选择怎样的坐标系,曲线的几何性质是不变的。教学时应向学生讲清图形本身的性质与坐标系的选择无关,把曲线不同位置的性质与曲线本身的性质区别开来。4。双曲线(1)要求恰当:重点是椭圆,双曲线的要求层次:了解(2)突出类比,如导言中的类比提出问题、研究过程中从结论、过程、方法各个层面与椭圆类比(3)注意性质部分的“范围“与原教材的区别:更为精确的限制,为渐近线的引入作铺垫(4)双曲线离心率几何意义的认识:与椭圆类比提出问题,通过数形结合的分析发现结论5。抛物线(1)注意与椭圆、双曲线的联系与区别(2)建立抛物线标准方程时坐标系的理性选择6。圆锥曲线的统一定义生长点:抛物线过程:特殊-------------------一般第2。5节的思考的功能(1)代数形式表达的几何意义的价值;(2)多角度认识同一数学对象设置意图:整体意识、数学内在的和谐、统一美7。曲线与方程(1)专列一节:突出解析几何的基本思想概念建立方程探求性质(2)概念:从特殊曲线的方程(如圆、直线、圆锥曲线等)概念中抽象出注意:原教材先曲线方程的概念再研究特殊曲线的方程:逻辑结构与认知结构的区别(3)两曲线相交的问题的说明特殊、简单的,不涉及一般情形8。文理科的区别(1)圆锥曲线的概念部分:文科直接说明(2)文科对抛物线只作“了解”(4)文科对“曲线与方程”不作要求(3)对“统一定义”,文科作为性质了解,而理科作为定义研究(5)文科在例、习题上要求降低9。特别说明:与原教材比较的几个变化:(1)结构体系变化了总体编排结构(2)处理方法变化了符合认知规律,暴露思维过程(3)文理分科要求(4)增加了丰富的“思考”、“探究”和开放性的问题,为学生个性发展提供了空间