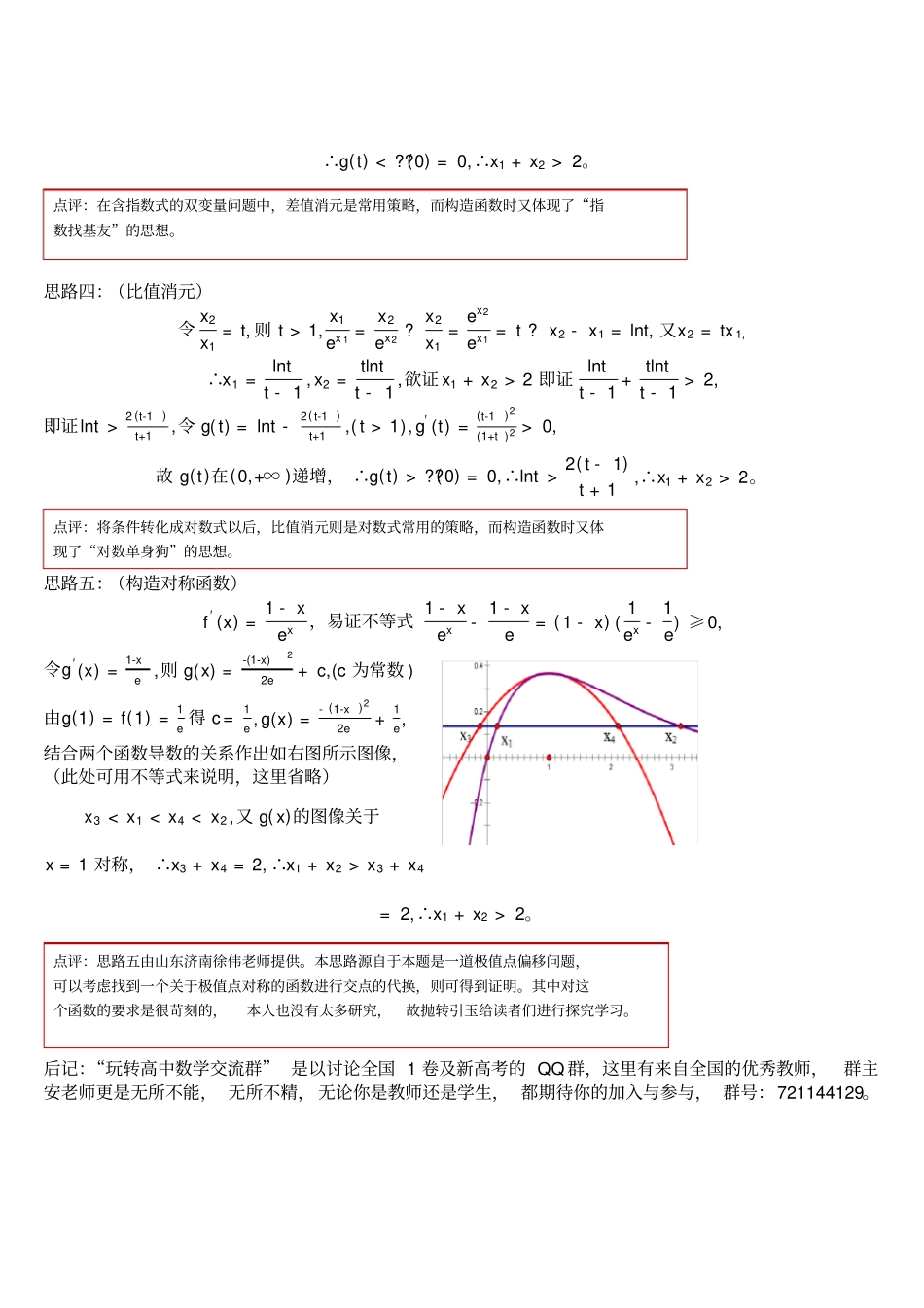
再次例谈导数压轴题中双变量问题的常用解法长沙市明达中学吴祥云今日在“玩转高中数学交流群”中,由河南的贾老师提供一常规题,很多老师作出了不同的解答,我在这里把它们总结起来,供大家交流学习。题目虽然简单,但是方法的讲述由浅入深,学生会更容易接受一些。闲话少说,先上题:已知函数f(x)=xex,f(x1)=f(x2),x1≠x2,求证:x1+x2>2.解析:f′(x)=1-xex,易得f(x)在(-∞,1)递增,(1,+∞)递减,其图像如图,为了更好的看图,横纵轴单位长度取得不同,不妨设0g(1)=0,即f(2-x)>f(x),∴f(2-x1)>f(x1)=f(x2),又2-x1>1,x2>1,f(x)在(1,+∞)递减,∴2-x12。思路二:(极值点偏移+对数平均不等式)f(x1)=f(x2)?x1ex1=x2ex2?lnx1-x1=lnx2-x2?lnx1-lnx2=x1-x2?x1-x2lnx1-lnx2=1,由对数平均不等式x1-x2lnx1-lnx21,即x1+x2>2。思路三:(差值消元)令x2-x1=t>0,x1ex1=x2ex2?x2x1=ex2ex1=ex2-x1=et?x1=tet-1,x2=tet-1+t,∴x1+x2=2tet-1+t,欲证x1+x2>2即证2tet-1+t<2即et(2-t)2+t<1,令g(t)=et(2-t)2+t,则g′(t)=et(-t2)(2+t)2<0,故g(t)在(0,+∞)递减,点评:构造对称函数为极值点偏移问题的通法。点评:含指数或者对数的不等式问题中,指对互化是常用技巧,而对数平均不等的功能更是巨大。∴g(t)2。思路四:(比值消元)令x2x1=t,则t>1,x1ex1=x2ex2?x2x1=ex2ex1=t?x2-x1=lnt,又x2=tx1,∴x1=lntt-1,x2=tlntt-1,欲证x1+x2>2即证lntt-1+tlntt-1>2,即证lnt>2(t-1)t+1,令g(t)=lnt-2(t-1)t+1,(t>1),g′(t)=(t-1)2(1+t)2>0,故g(t)在(0,+∞)递增,∴g(t)>??(0)=0,∴lnt>2(t-1)t+1,∴x1+x2>2。思路五:(构造对称函数)f′(x)=1-xex,易证不等式1-xex-1-xe=(1-x)(1ex-1e)≥0,令g′(x)=1-xe,则g(x)=-(1-x)22e+c,(c为常数)由g(1)=f(1)=1e得c=1e,g(x)=-(1-x)22e+1e,结合两个函数导数的关系作出如右图所示图像,(此处可用不等式来说明,这里省略)x3x3+x4=2,∴x1+x2>2。后记:“玩转高中数学交流群”是以讨论全国1卷及新高考的QQ群,这里有来自全国的优秀教师,群主安老师更是无所不能,无所不精,无论你是教师还是学生,都期待你的加入与参与,群号:721144129。点评:在含指数式的双变量问题中,差值消元是常用策略,而构造函数时又体现了“指数找基友”的思想。点评:将条件转化成对数式以后,比值消元则是对数式常用的策略,而构造函数时又体现了“对数单身狗”的思想。点评:思路五由山东济南徐伟老师提供。本思路源自于本题是一道极值点偏移问题,可以考虑找到一个关于极值点对称的函数进行交点的代换,则可得到证明。其中对这个函数的要求是很苛刻的,本人也没有太多研究,故抛转引玉给读者们进行探究学习。