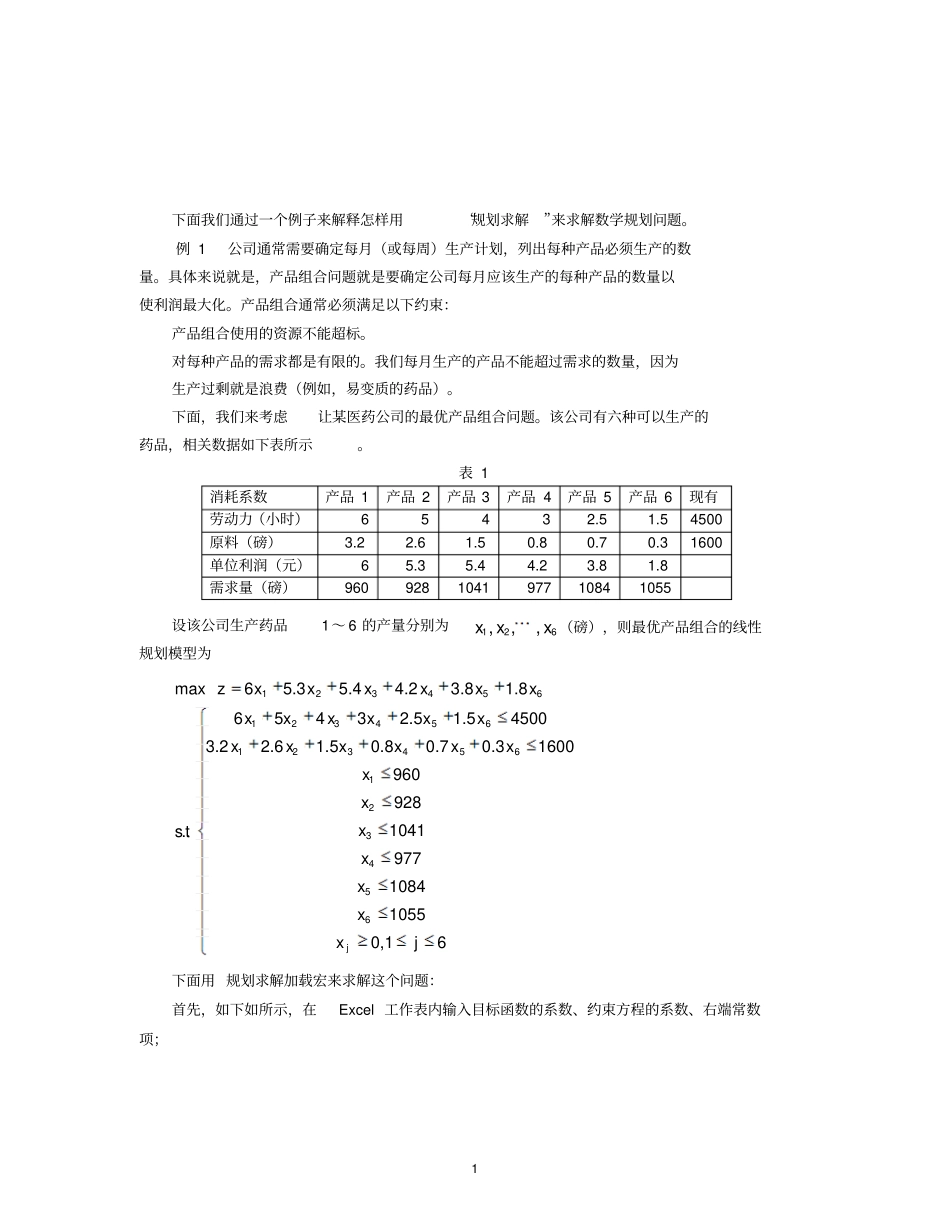
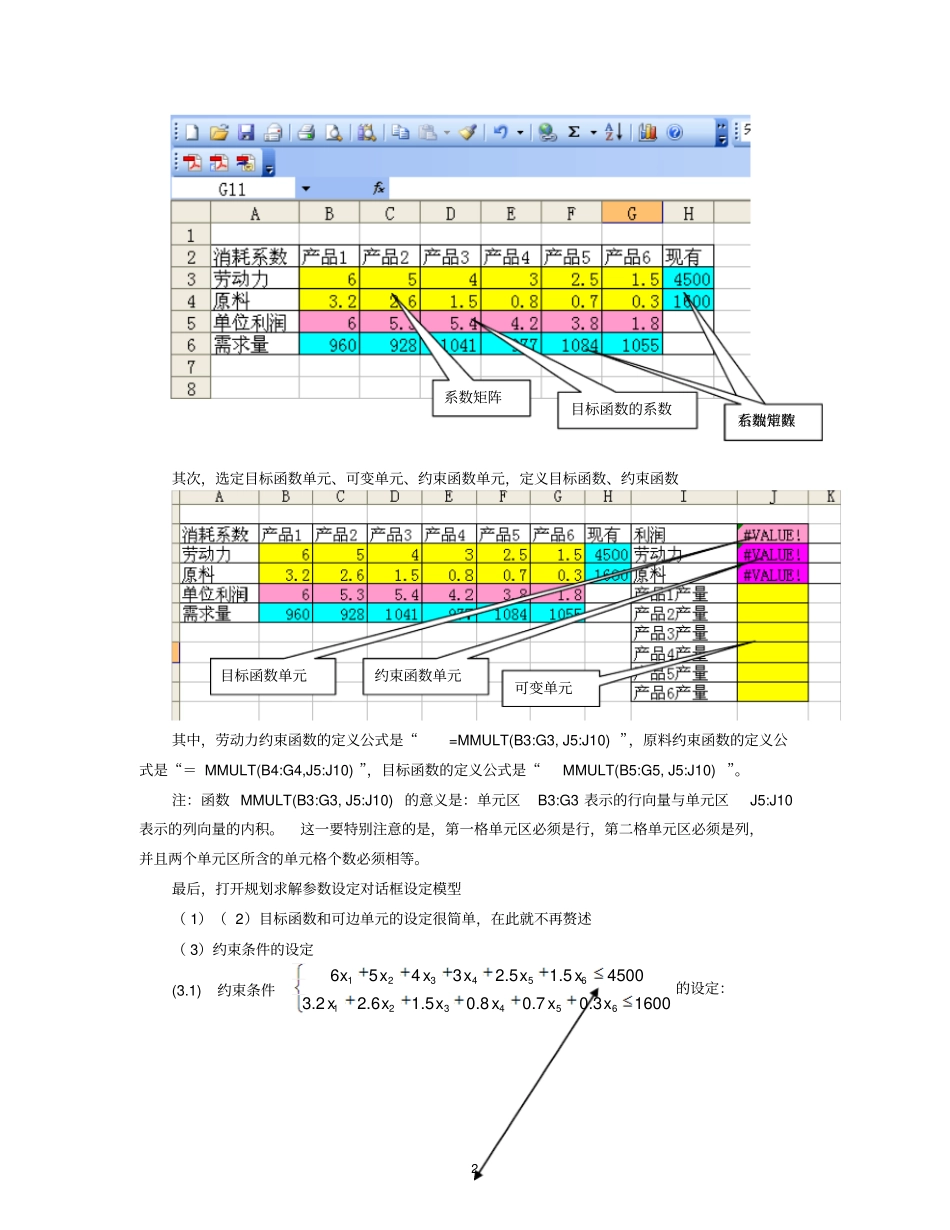
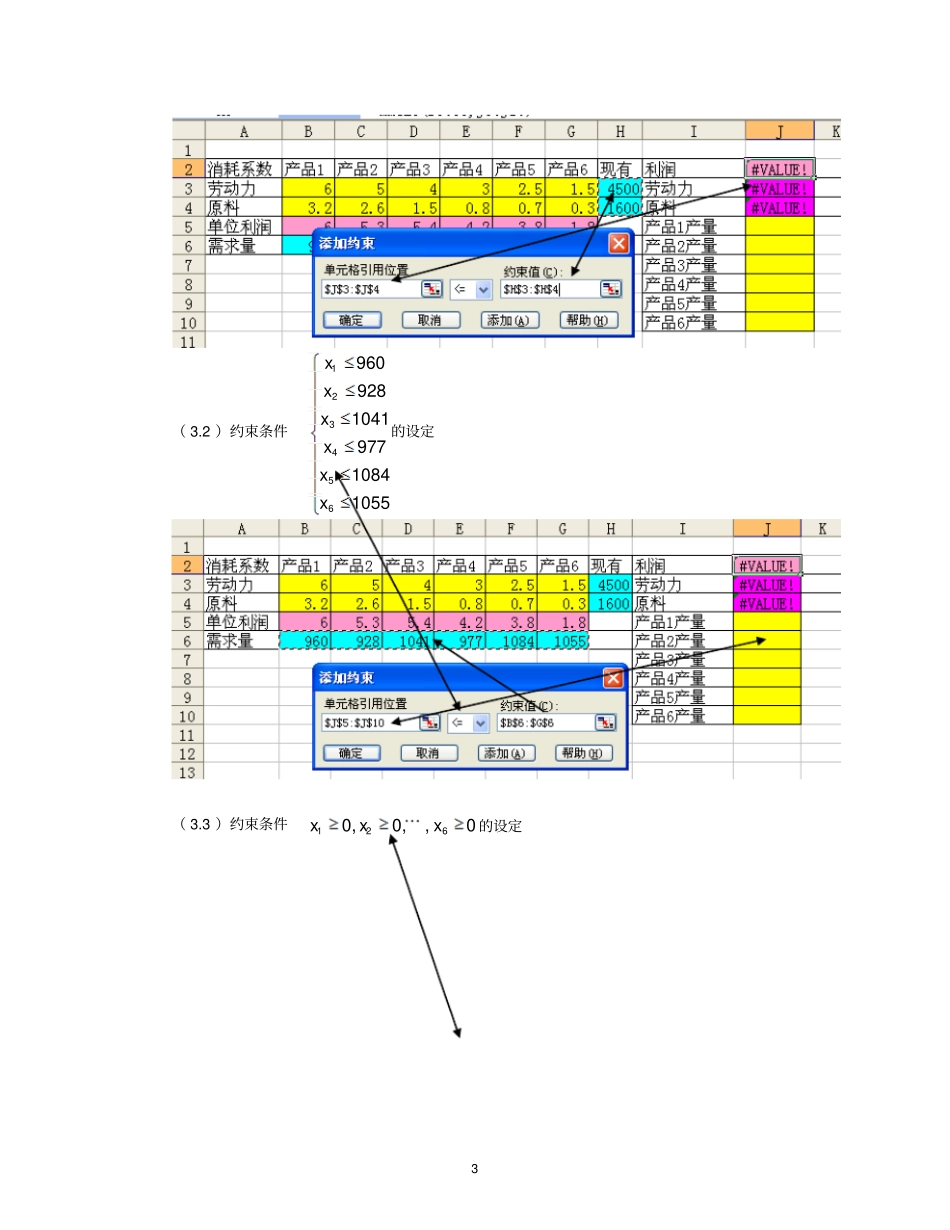
1 下面我们通过一个例子来解释怎样用“规划求解”来求解数学规划问题。例 1公司通常需要确定每月(或每周)生产计划,列出每种产品必须生产的数量。具体来说就是,产品组合问题就是要确定公司每月应该生产的每种产品的数量以使利润最大化。产品组合通常必须满足以下约束:产品组合使用的资源不能超标。对每种产品的需求都是有限的。我们每月生产的产品不能超过需求的数量,因为生产过剩就是浪费(例如,易变质的药品)。下面,我们来考虑让某医药公司的最优产品组合问题。该公司有六种可以生产的药品,相关数据如下表所示。表 1 消耗系数产品 1 产品 2 产品 3 产品 4 产品 5 产品 6 现有劳动力(小时)6 5 4 3 2.5 1.5 4500 原料(磅)3.2 2.6 1.5 0.8 0.7 0.3 1600 单位利润(元)6 5.3 5.4 4.2 3.8 1.8 需求量(磅)960 928 1041 977 1084 1055 设该公司生产药品1~ 6 的产量分别为126,,,x xx (磅),则最优产品组合的线性规划模型为123456123456123456123456max65.35.44.23.81.865432.51.545003.22.61.50.80.70.316009609281041..977108410550,16jzxxxxxxxxxxxxxxxxxxxxxstxxxxj下面用 规划求解加载宏来求解这个问题:首先,如下如所示,在Excel 工作表内输入目标函数的系数、约束方程的系数、右端常数项;2 其次,选定目标函数单元、可变单元、约束函数单元,定义目标函数、约束函数其中,劳动力约束函数的定义公式是“=MMULT(B3:G3, J5:J10) ”,原料约束函数的定义公式是“= MMULT(B4:G4,J5:J10) ”,目标函数的定义公式是“MMULT(B5:G5, J5:J10) ”。注:函数 MMULT(B3:G3, J5:J10) 的意义是:单元区B3:G3 表示的行向量与单元区J5:J10表示的列向量的内积。这一要特别注意的是,第一格单元区必须是行,第二格单元区必须是列,并且两个单元区所含的单元格个数必须相等。最后,打开规划求解参数设定对话框设定模型( 1)( 2)目标函数和可边单元的设定很简单,在此就不再赘述( 3)约束条件的设定(3.1) 约束条件12345612345665432.51.545003.22.61.50.80.70.31600xxxxxxxxxxxx的设定:系数矩阵目标函数的系数系数矩阵右端常数可变单元约束函数单元目标函数单元3 ( 3.2 )约束条件123456960928104197710841055xxxxxx的设定( 3.3 )约束条件1260,0,,0xxx的设定4 这里值得注意的是:我们采用向量的形式设定同向不等式,并且不等式两边可以一个时行向量,另一个是列向...