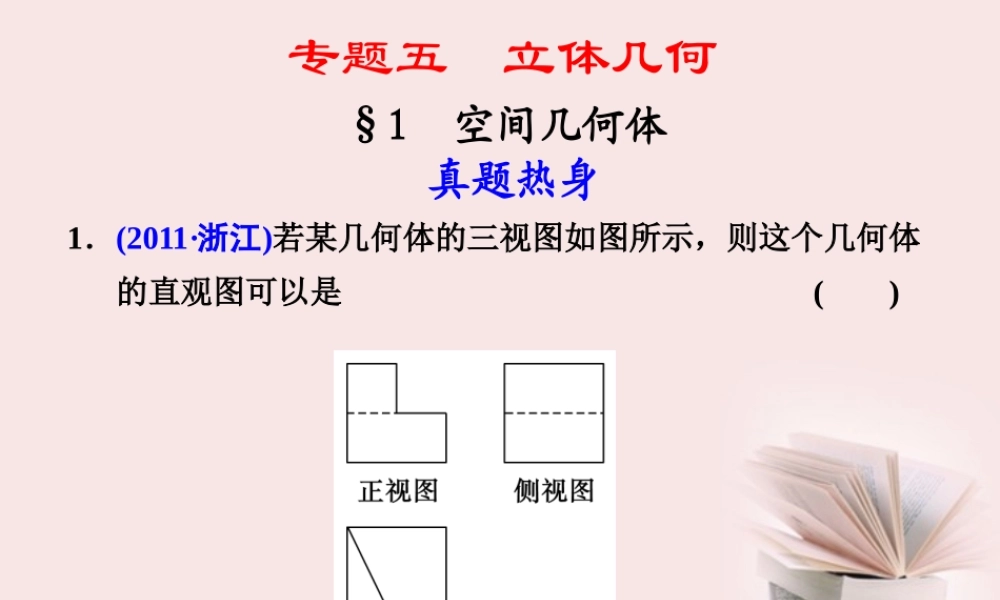
专题五 立体几何 §1 空间几何体 真题热身 1.(2011·浙江)若某几何体的三视图如图所示,则这个几何体 的直观图可以是 ( ) 解析 A,B 的正视图不符合要求,C 的俯视图显然不符合要求,答案选 D. 答案 D 2.(2011·湖北)设球的体积为 V1,它的内接正方体的体积为 V2, 下列说法中最合适的是 ( ) A.V1 比 V2 大约多一半 B.V1 比 V2 大约多两倍半 C.V1 比 V2 大约多一倍 D.V1 比 V2 大约多一倍半 解析 设球半径为 R,则 V1=43πR3.设正方体棱长为 a,则 V2=a3.又 2R= 3a,∴R= 32 a. ∴V1=4π3 ( 32 a)3= 32 πa3. ∴V1-V2=( 32 π-1)a3≈1.7a3. D3.(2011·天津)一个几何体的三视图如图所示(单位:m),则该 几何体的体积为________m3. 解析 此几何体是由一个长为 3,宽为 2,高为 1 的长方体与底面直径为 2,高为 3 的圆锥组合而成的,故 V=V 长方体+V 圆锥=3×2×1+π3×12×3=(6+π)m3. 答案 (6+π) 4. (2011·四川)如图,半径为 4 的球 O 中有一内接圆柱,当圆 柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是 ________. 解析 方法一 圆柱的轴截面如图所示,设球的半径与圆柱的高所成的角为 α,则圆柱底面半径为 4sin α, 高为 8cos α, ∴S 圆柱侧=2π·4sin α·8cos α=32πsin 2α. 当 sin 2α=1 时,S 圆柱侧最大为 32π. 此时 S 球表-S 圆柱侧=4π·42-32π=32π. 方法二 设圆柱底面半径为 r,则其高为 2 R2-r2, ∴S 圆柱侧=2πr·2 R2-r2=4π r2(R2-r2)≤ 4πr2+(R2-r2)2=2πR2(当且仅当 r2=R2-r2,即 r= 22 R 时取 “=”). 又 R=4,∴S 圆柱侧最大为 32π. 此时 S 球表-S 圆柱侧=4π·42-32π=32π. 答案 32π 考点整合 1.棱柱、棱锥 (1)棱柱的性质 侧棱都相等,侧面是平行四边形;两个底面与平行于底面的截面是全等的多边形;过不相邻的两条侧棱的截面是平行四边形;直棱柱的侧棱长与高相等且侧面与对角面是矩形. (2)正棱锥的性质 侧棱相等,侧面是全等的等腰三角形,斜高相等;棱锥的高、斜高和斜高在底面内的射影构成一个直角三角形;棱锥的高、侧棱和侧棱在底面内的射影也构成一个直角三角形;某侧面的斜高、侧棱及底面边长的一半也构成一个直角三角形;侧棱在底面内的射影、斜高在底面内的射影及底面边长的一半也构成一个直...