高一数学 正弦函数、余弦函数的性质 课件VIP免费

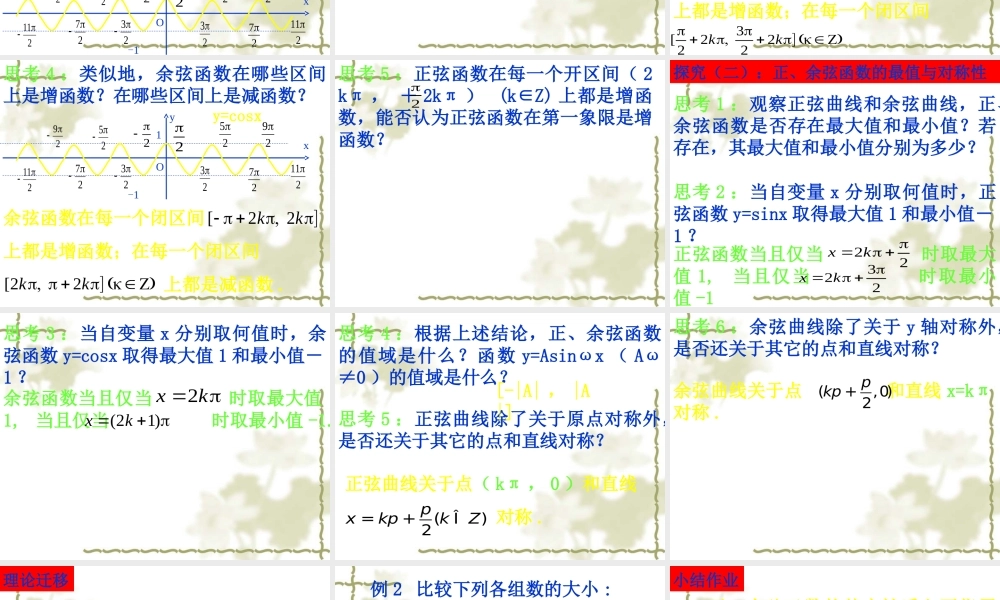
1.4.2 正弦函数、余弦函数的性质 第二课时问题提出1. 周期函数是怎样定义的？ 对于函数 f(x) ，如果存在一个非零常数 T ，使得当 x 取定义域内的每一个值时，都有 f(x +T)=f(x), 那么函数 f(x) 就叫做周期函数，非零常数T 就叫做这个函数的周期 .2. 正、余弦函数的最小正周期是多少？函数 和 的最小正周期是多少？sin()yAxwj=+cos()yAxwj=+(0,0)Aw¹>3. 周期性是正、余弦函数所具有的一个基本性质，此外，正、余弦函数还具有哪些性质呢？我们将对此作进一步探究 .探究（一）：正、余弦函数的奇偶性和单调性思考 1 ：观察下列正弦曲线和余弦曲线的对称性，你有什么发现？y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinxxyO1-1222222222222y=cosx思考 2 ：上述对称性反映出正、余弦函数分别具有什么性质？如何从理论上加以验证？正弦函数是奇函数，余弦函数是偶函数 .思考 3 ：观察正弦曲线，正弦函数在哪些区间上是增函数？在哪些区间上是减函数？如何将这些单调区间进行整合？y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinx正弦函数在每一个闭区间上都是增函数；在每一个闭区间 上都是减函数 .[222kk [222kk 思考 4 ：类似地，余弦函数在哪些区间上是增函数？在哪些区间上是减函数？余弦函数在每一个闭区间上都是增函数；在每一个闭区间 上都是减函数 .[22kk   [22kk xyO1-1222222222222y=cosx思考 5 ：正弦函数在每一个开区间（ 2kπ ， ＋ 2kπ ） (k∈Z) 上都是增函数，能否认为正弦函数在第一象限是增函数？2探究（二）：正、余弦函数的最值与对称性 思考 1 ：观察正弦曲线和余弦曲线，正、余弦函数是否存在最大值和最小值？若存在，其最大值和最小值分别为多少？思考 2 ：当自变量 x 分别取何值时，正弦函数 y=sinx 取得最大值 1 和最小值－1 ？正弦函数当且仅当 时取最大值 1, 当且仅当 时取最小值 -1 2xk  2xk  思考 3 ：当自变量 x 分别取何值时，余弦函数 y=cosx 取得最大值 1 和最小值－1 ？余弦函数当且仅当 时取最大值1, 当且仅当 时取最小值 -1. 2xk...