高中数学 24 平面向量的数量积知识表格素材 新人教版必修4 素材VIP免费

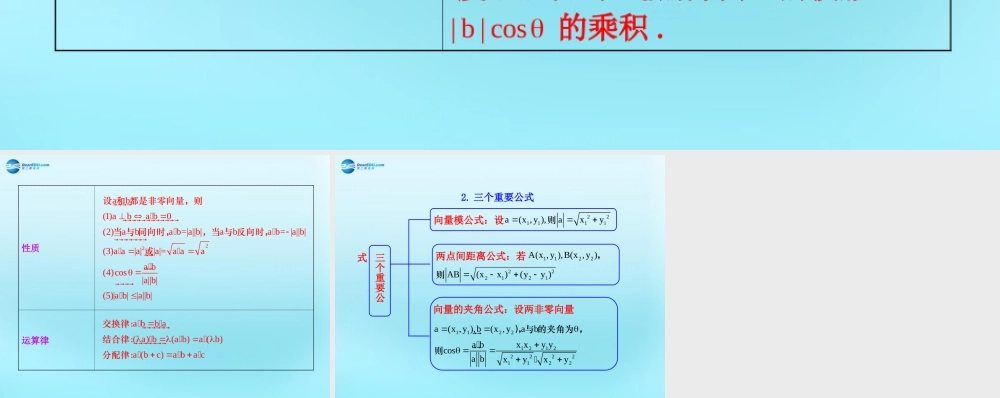
1. 平面向量的数量积定义 几何意义 已知两个非零向量 与 ，我们把数量 叫做 与 的数量积 . 记作 ，即 ，其中 θ 是 与 的夹角，零向量与任一向量的数量积为 0.ab| a || b | cosaba ba b | a || b | cosab 叫做向量 在 方向上（ 在 方向上）的投影 .的几何意义是数量积 等于 的长度 与 在 的方向上的投影 的乘积 .ab| a | cos (| b | cos )baa ba ba| a |ba| b | cos性质运算律22ab(1)aba b0(2)aba b=|a||b|aba b= |a||b|(3)a a|a||a|= a aaa b(4)cos|a||b|(5)|a b||a||b| 设 和 都是非零向量，则当 与 同向时，，当 与 反向时，或a bb a( a) b(a b)a ( b)a (bc)a ba c交换律：结合律：分配律：2. 三个重要公式 三个重要公式向量模公式：设221111a(x ,y ),axy则两点间距离公式：若1122A(x ,y ),B(x ,y )，222121AB(xx )(yy )�则向量的夹角公式：设两非零向量1122121222221122a(x ,y ),b(x ,yabx xy ya bcosa bxyxy )，与 的夹角为 ，则