高中数学 平面向量的数量积课件 新人教A版必修4 课件VIP免费

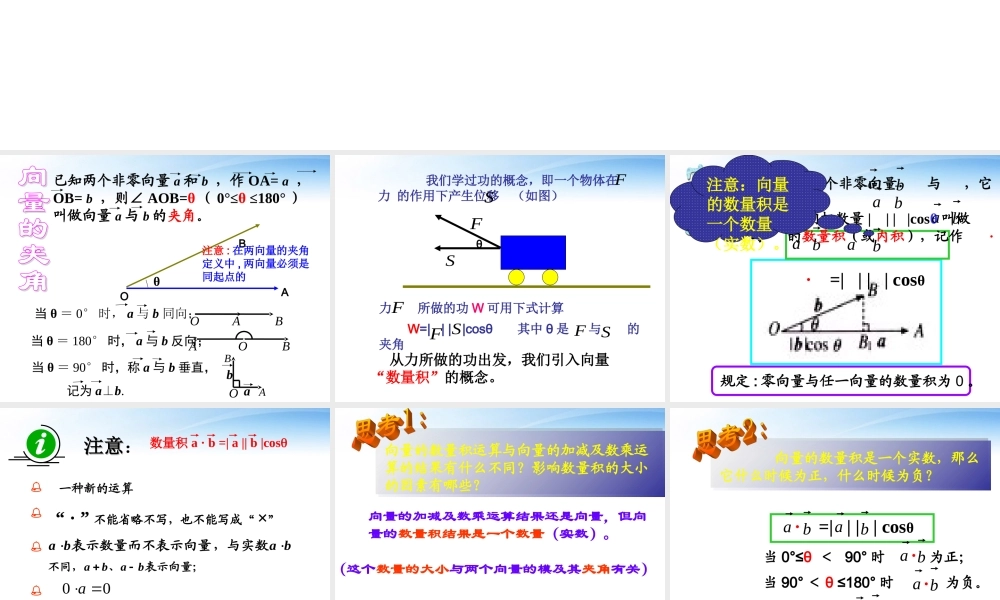
y2.4 平面向量的数量积已知两个非零向量 a 和 b ，作 OA= a ， OB= b ，则∠ AOB=θ （ 0°≤θ ≤180° ）叫做向量 a 与 b 的夹角。OBAθ当 θ ＝ 0° 时， a 与 b 同向；OAB当 θ ＝ 180° 时， a 与 b 反向；OABB当 θ ＝ 90° 时，称 a 与 b 垂直， 记为 a⊥b.OAab注意 : 在两向量的夹角定义中 , 两向量必须是同起点的 我们学过功的概念，即一个物体在力 的作用下产生位移 （如图）θ 从力所做的功出发，我们引入向量“数量积”的概念。S�F�S�S�F�力 所做的功 W 可用下式计算 W=| | | |cosθ 其中 θ 是 与 的夹角F�F�S�F�S� 已知两个非零向量 与 ，它们的夹角为 θ ，我们把数量 | | | |cosθ 叫做 与 的数量积（或内积），记作 · · =| | | | cosθaaaaaa bbbbbb注意：向量的数量积是一个数量（实数）。规定 : 零向量与任一向量的数量积为 0 。注意注意： 数量积 a · b =| a || b |cosbaba，与实数表示数量而不表示向量表示向量；、不同，baba00a    注意公式变形，知三求一 .  “ · ” 不能省略不写，也不能写成“ ×” 一种新的运算向量的数量积运算与向量的加减及数乘运算的结果有什么不同？影响数量积的大小的因素有哪些？向量的加减及数乘运算结果还是向量，但向量的数量积结果是一个数量（实数）。（这个数量的大小与两个向量的模及其夹角有关） 向量的数量积是一个实数，那么它什么时候为正，什么时候为负？ · =| | | | cosθaabb当 θ =90° 时 为零。a b·当 90° ＜ θ ≤180° 时 为负。a b·当 0°≤θ ＜ 90° 时 为正；a b·解： a·b = |a| |b|cosθ = 5×4×cos120° =5×4× （ -1/2 ） = － 10例 1 已知 |a|=5 ， |b|=4 ， a 与 b的夹角 θ=120° ，求 a·b 。 ,1:平行且方向相同与因为解BCAD.0的夹角为与BCAD91330cosBCADBCAD 且方向相反平行与,CDAB2 180的夹角是与CDAB16144180cosCDABCDAB ,60ADAB3的夹角是与120的夹角是与DAAB62134120cos DAABDAAB典型例题分析进行向量数量积计算时 , 既要考虑向量的模 , ...