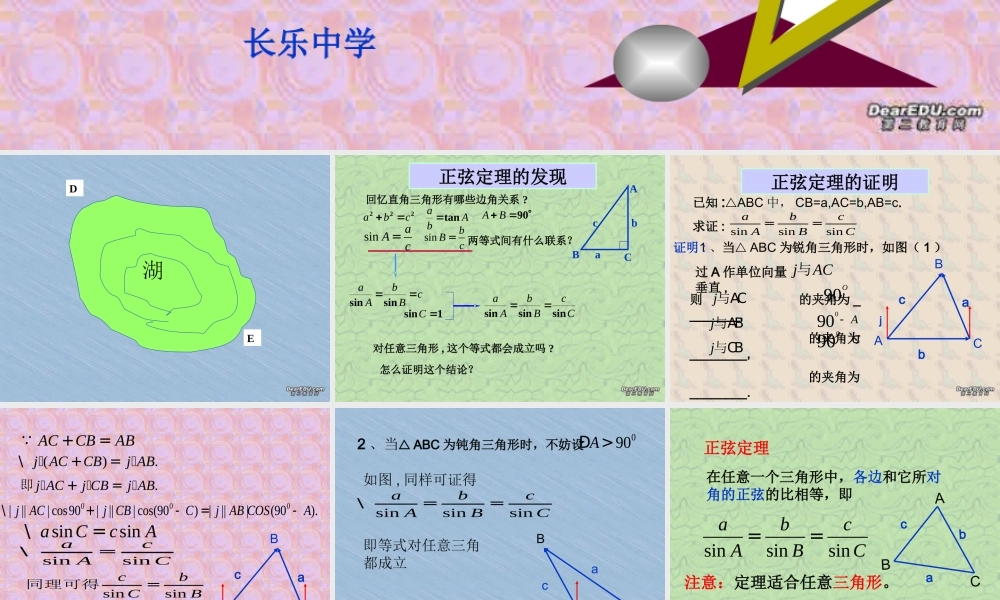
长乐中学DE湖正弦定理的发现回忆直角三角形有哪些边角关系 ? ABCcba222cbasinaAc=sinbBc=Abatan90BA两等式间有什么联系?cBbAasinsin1sinCCcBbAasinsinsin对任意三角形 , 这个等式都会成立吗 ?怎么证明这个结论?正弦定理的证明1 、当 ABC 为锐角三角形时,如图( 1 )证明 :过 A 作单位向量 垂直 ,jAC��与则 的夹角为 ________, 的夹角为________, 的夹角为________.j��与ACj��与ABj��与CB已知 :ABC 中, CB=a,AC=b,AB=c.求证 : sinsinsinabcABC==90O090A-090C-ACBabcjACBabcACCBAB+=�().j ACCBj AB\+=��.j ACj CBj AB+=��即000| ||| cos90| ||| cos(90)| |||(90).jACj CBCjAB COSA\+-=-��sinsinaCcA\=sinsinacAC\=sinsincbCB=同理可得sinsinsinabcABC\==2 、当 ABC 为钝角三角形时,不妨设090AÐ >ABCabc如图 , 同样可证得sinsinsinabcABC\==即等式对任意三角都成立正弦定理在任意一个三角形中,各边和它所对角的正弦的比相等,即sinsinsinabcABC==注意:定理适合任意三角形。ABCacb例1、在ABC中,已知 c=10,A=45oC= 30o , 求 b( 保留两个有效数字)解 :sinsinbcBC=B= 180°-(A+C)= 180°-(45°+ 30°)= 105°sin10sin105sinsin30oocBbC\==100.966190.5´=»4、例题讲解例 2 、 在 ABC 中,已知 a = 60 , b = 50 , A=38° ,求 B (精确到 1° )和 c (保留两个有效数字)。解:已知 b
\>而148OB\=2132oB =194OC\=210oC =11sin50sin9481.02sinsin38ooaCcA\==»22sin50sin1014.10sinsin38ooaCcA\==»变式 2 、 已知 a = 25 , b = 50 , A=38° ,则这样的 ABC 是否存在?sin50sin3830.78obA ==30.78sin125B\=> 无解概括 : 利用正弦定理可以解哪些条件下的三角形问题 ?两类 : (1) 、已知两角和任一边 , 求一角和其他两条边 .(2) 、已知两边和其中一边的对角 , 求另一边的对角 ( 进而求其他的角和...