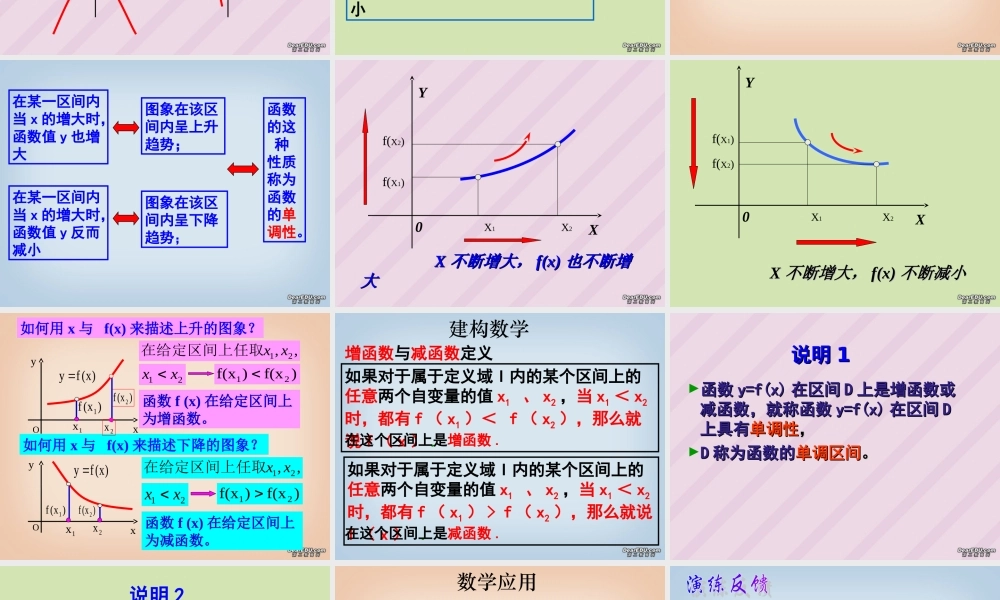
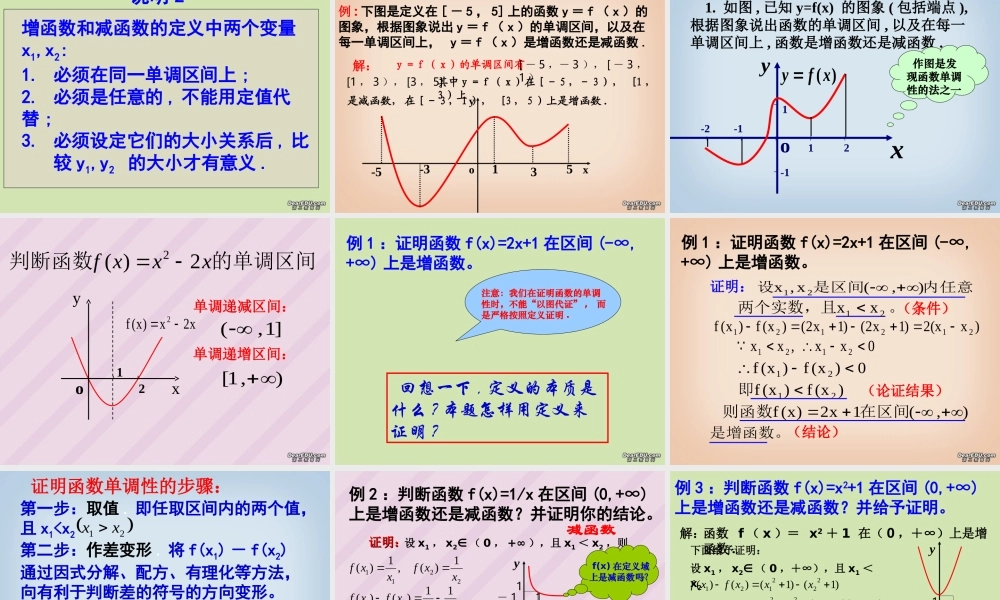
函数的单调性函数的单调性 创设情境,引入新课 建立函数的目的是研究函数值与自变量的关系,自变量的变化对函数值变化的影响是经常受到关注的问题.例如水位的涨落随时间变化的规律,是防涝抗旱工作中必须解决的实际问题.下面我们开始研究函数在这方面的一个主要性质——函数的单调性.下面是某一天温度的变化图象:tTo369 12 15 18 2124134-12-25( 小时 )( OC )141 、在上午 6 时的气温约是多少?全天的最高、最低气温分别是多少?2 、什么时刻气温是 0 度?3 、在什么时段内,气温在 0 度以上?4 、说出这一天的气温变化趋势,怎样用数 学语言刻画这一特征。问题 1:问题 1 、观察自己所作函数图象,并指出图象的变化的趋势学学生生活活动动自己作出下列函数的图象:(1)1yx . (2)22yx. 1(4)yx. 2(3)yx. Oxy2x2y21yOxx1y Oxy1xy1-1yOx2xy问题 2 :你能明确说出“图象呈下降趋势”的意思吗?在某一区间内;当 x 的增大时,函数值 y 反而减小学生讨论图象在该区间内呈下降趋势;问题 3 :你能明确说出“图象呈上升趋势”的意思吗?在某一区间内;当 x 的增大时,函数值 y 也增大学生讨论结论图象在该区间内呈上升趋势;在某一区间内当 x 的增大时,函数值 y 反而减小图象在该区间内呈下降趋势;在某一区间内当 x 的增大时,函数值 y 也增大图象在该区间内呈上升趋势;函数的这 种性质称为函数的单调性。 XX 不断增大,不断增大, f(x)f(x) 也不断增也不断增大大0 XYX1X2f(X1)f(X2)Y X0 XX 不断增大,不断增大, f(x)f(x) 不断减小不断减小X1X2f(X2)f(X1),,21 xx在给定区间上任取21xx )f(x)f(x21 函数 f (x) 在给定区间上为增函数。Oxy)x(fy 如何用 x 与 f(x) 来描述上升的图象?)x(f11x如何用 x 与 f(x) 来描述下降的图象?,,21 xx在给定区间上任取21xx 函数 f (x) 在给定区间上为减函数。)f(x)f(x21 )x(f1)x(f2)x(fy Oxy1x2x)x(f22x如果对于属于定义域 I 内的某个区间上的任意两个自变量的值 x1 、 x2 ,当 x1 < x2时,都有 f ( x1 )< f ( x2 ),那么就说 f ( x ) .在这个区间上是增函数 .如果对于属于定义域 I 内的某个区间上的任意两个自变量的值 x1 、 x2 ,当 x1 < x2时,都有 f ( x1 ) > f ( x2 ),那么就说f ( x ) .在这个区间上是减函数...