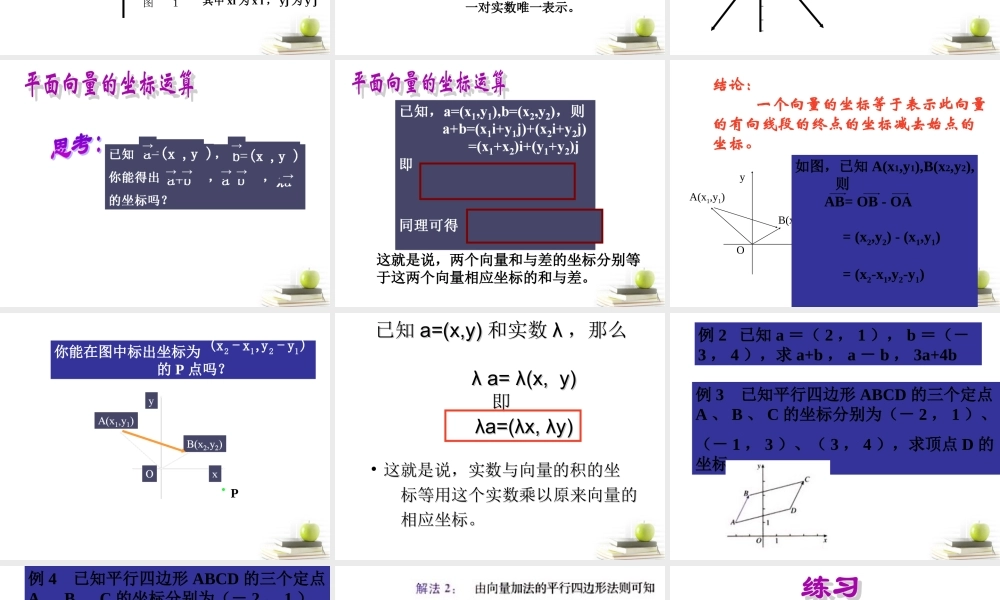
1 、平面向量的坐标表示与平面向量分解定理的关系。2 、平面向量的坐标是如何定义的?3 、平面向量的运算有何特点? 类似地,由平面向量的分解定理,对于平面上的任意向量 ,均可以分解为不共线的两个向量 和 使得a→1 1λa→2 2λ a→=a→1 1λa→ +2 2λ a→ 在不共线的两个向量中,垂直是一种重要是情形,把一个向量分解为两个互相垂直的向量,叫做把向量正交分解。 我们知道,在平面直角坐标系,每一个点都可用一对有序实数(即它的坐标)表示,对直角坐标平面内的每一个向量,如何表示? 在平面上,如果选取互相垂直的向量作为基底时,会为我们研究问题带来方便。 我们把( x,y) 叫做向量 a 的(直角)坐标,记作 a=(x , y), 其中 x 叫做 a 在 x 轴上的坐标, y 叫做 a 在 y 轴上的坐标,( x ,y )叫做向量的坐标表示。ayjiO图 1xxiyj a=xi+yj( 1 ,0 )( 0 ,1 )( 0 ,0 )i=j=0=→→→其中 i , j 为向量 i , j→ →→→→ayjiO图 1xxiyj其中 xi 为 x i , yj 为 y j→→yxOyxjA ( x,y )a如图,在直角坐标平面内,以原点 O 为起点作 OA=a ,则点 A 的位置由 a 唯一确定。设 OA=xi+yj ,则向量 OA 的坐标( x,y) 就是点 A 的坐标;反过来,点 A 的坐标( x,y) 也就是向量 OA的坐标。因此,在平面直角坐标系内,每一个平面向量都可以用一对实数唯一表示。i例 1 如图,用基底 i , j 分别表示向量 a 、 b 、 c 、d , 并求出它们的坐标。jyxOiaA1AA2bcd解:由图 3 可知 a=AA1+AA2=2i+3j, ∴ a=(2,3) 同理, b=-2i+3j=(-2,3) c=-2i-3j=(-2,-3)d=2i-3j=(2,-3)这就是说,两个向量和与差的坐标分别等于这两个向量相应坐标的和与差。结论: 一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标。yxOB(x2,y2)A(x1,y1)如图,已知 A(x1,y1),B(x2,y2), 则 AB= OB - OA = (x2,y2) - (x1,y1) = (x2-x1,y2-y1)你能在图中标出坐标为 的 P 点吗?2121(x - x ,y - y )P已知已知 a=(x,y)a=(x,y) 和实数和实数 λλ ,那么,那么 λλ a= a= λλ(x, y)(x, y)即即 λa=(λx, λy)λa=(λx, λy)• 这就是说,实数与向量的积的坐这就是说,实数与向量的积的坐 标等用这个实数乘以原来向量的标等用这个实数乘以原来向量的 相应坐标。相应坐标。例 2 已知 a =( 2 ,...