高一数学正弦 余弦函数的图象 课件VIP免费

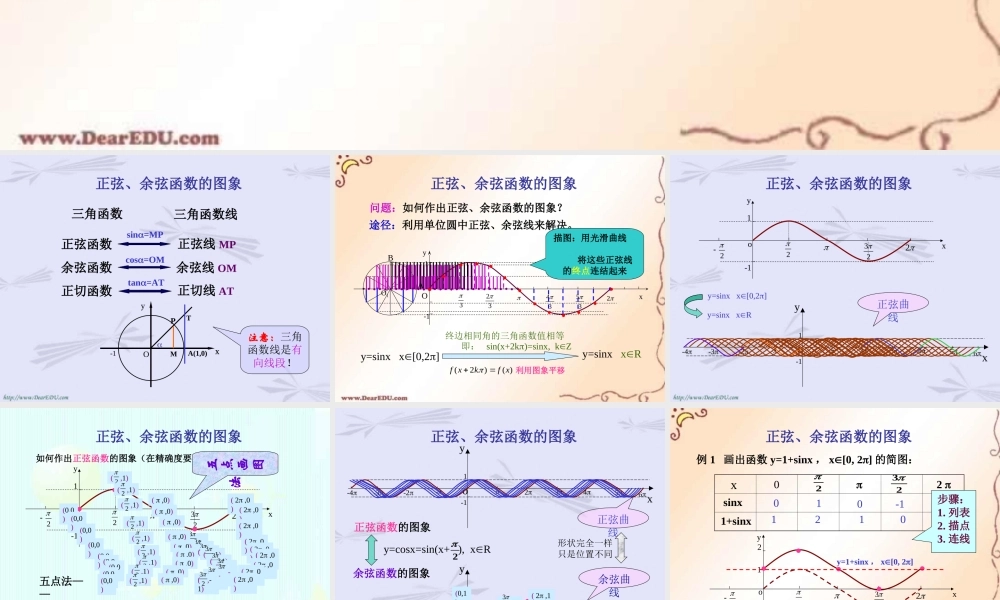
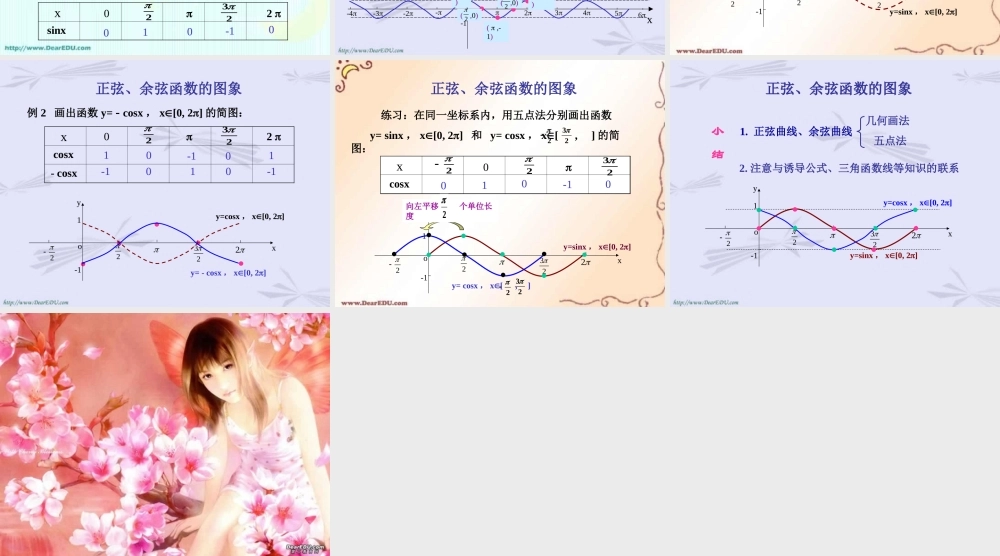
正弦 余弦函数的图象 三角函数三角函数线正弦函数余弦函数正切函数正弦线 MP 正弦、余弦函数的图象 yxO-1PMA(1,0)Tsin=MPcos=OMtan=AT注意：三角函数线是有向线段！余弦线 OM正切线 AT 正弦、余弦函数的图象 问题：如何作出正弦、余弦函数的图象？途径：利用单位圆中正弦、余弦线来解决。 y=sinx x[0,2]O1 O yx33234352-11y=sinx xR终边相同角的三角函数值相等 即： sin(x+2k)=sinx, kZ )()2(xfkxf描图：用光滑曲线 将这些正弦线的终点连结起来利用图象平移AB···· ········· 正弦、余弦函数的图象 x6yo--12345-2-3-41yxo1-122322y=sinx x[0,2]y=sinx xR正弦曲线 正弦、余弦函数的图象 yxo1-122322如何作出正弦函数的图象（在精确度要求不太高时）？(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)五点画图法五点法——(0,0)( ,1)2(  ,0)( ,1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0)(0,0)( ,1)2(  ,0)( ,-1)23( 2 ,0) x sinx223 0  2 010-10x6yo--12345-2-3-41 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 x6yo--12345-2-3-41y=cosx=sin(x+ ), xR2余弦曲线(0,1)( ,0)2(  ,-1)( ,0)23( 2 ,1)正弦曲线形状完全一样只是位置不同 正弦、余弦函数的图象 例 1 画出函数 y=1+sinx ， x[0, 2] 的简图： x sinx 1+sinx223 0  2 010-10 1 2 1 0 1 o1yx22322-12y=sinx ， x[0, 2]y=1+sinx ， x[0, 2]步骤：1. 列表2. 描点3. 连线 正弦、余弦函数的图象 例 2 画出函数 y= - cosx ， x[0, 2] 的简图： x cosx - cosx223 0  2 10-101 -1 0 1 0 -1 yxo1-122322y= - cosx ， x[0, 2]y=cosx ， x[0, 2] 正弦、余弦函数的图象 x sinx223 0  2 10-101 练习：在同一坐标系内，用五点法分别画出函数 y= sinx ， x[0, 2] 和 y= cosx ， x[ , ] 的简图：223o1yx22322-12y=sinx ， x[0, 2]y= cosx ， x[ , ] 223向左平移 个单位长度2 x cosx100-10223 0  2 正弦、余弦函数的图象 正弦、余弦函数的图象 小结1. 正弦曲线、余弦曲线几何画法 五点法2. 注意与诱导公式、三角函数线等知识的联系yxo1-122322y=sinx ， x[0, 2]y=cosx ， x[0, 2]