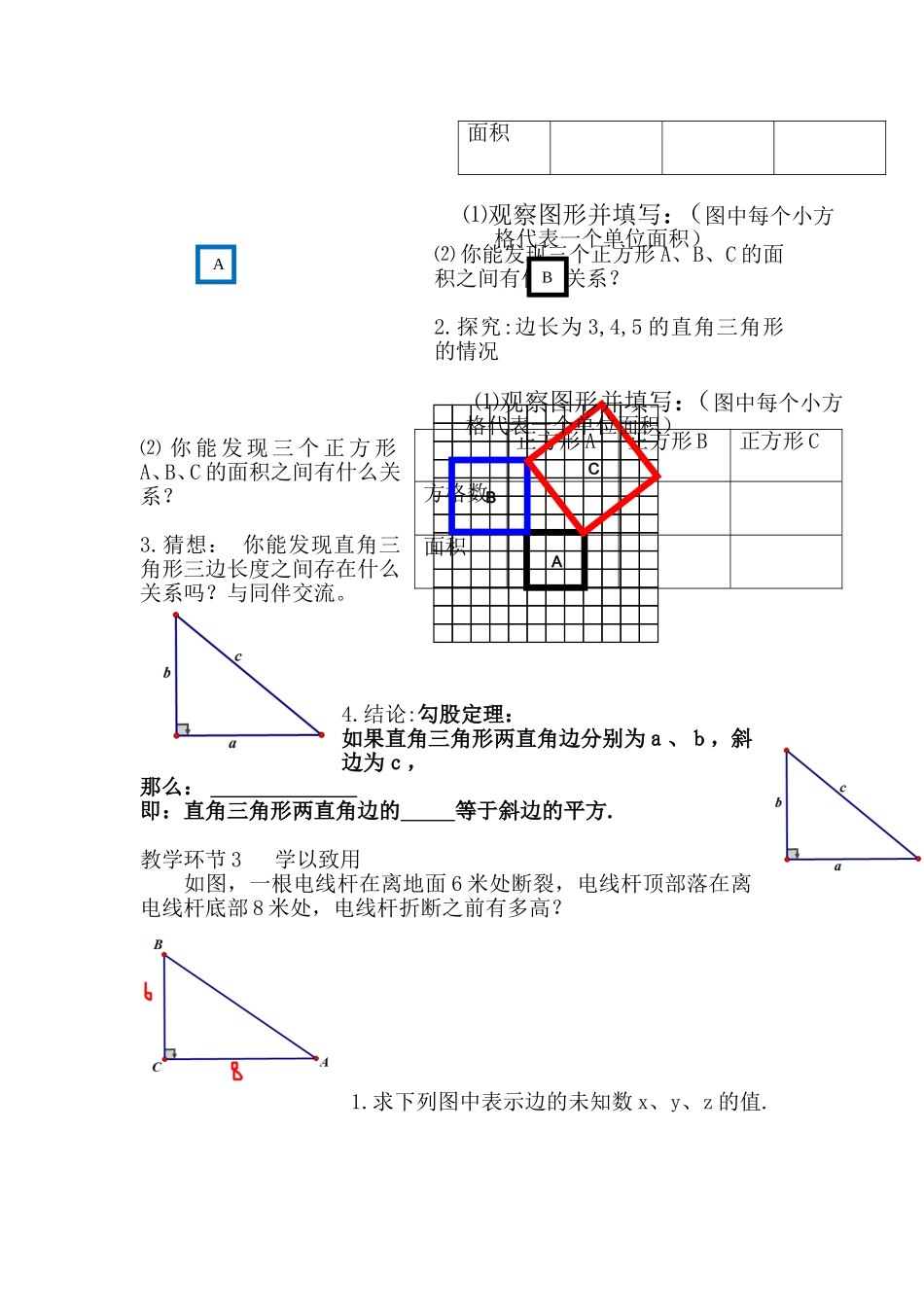
“探索勾股定理”教学设计一、教学目标:1.知识与技能:理解直角三角形的三边之间的数量关系,掌握勾股定理和它的简单应用。2.过程与方法:让学生经历“观察计算——猜想——归纳——验证”的数学思想,并体会“数形结合”和从特殊到一般的思想方法,进一步发展学生的说理和简单推理的意识及能力。3.情感、态度与价值观:通过对勾股定理历史的了解,激发学生的爱国情感,激发学习热情,培养学生的民族自豪感和主动探究意识,进一步体会数学与现实生活的紧密联系。二、教学重点难点:探索勾股定理的由来并能用它解决一些简单数学问题。三、教学方法:观察法、实验法、发现法、讲授法、练习法等。四、教学过程:教学环节 1 提出问题 引入新课如图,一根电线杆在离地面 6 米处断裂,电线杆顶部落在离电线杆底部 8 米处,电线杆折断之前有多高?教学环节 2 猜想与假设 1.探究:边长为 2 的等腰直角三角形的情况正方形 A正方形 B正方形 C方格数⑵ 你能发现三个正方形 A、B、C 的面积之间有什么关系?2.探究:边长为 3,4,5 的直角三角形的情况⑵ 你 能 发 现 三 个 正 方 形A、B、C 的面积之间有什么关系?3.猜想: 你能发现直角三角形三边长度之间存在什么关系吗?与同伴交流。4.结论:勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么: 即:直角三角形两直角边的 等于斜边的平方.教学环节 3 学以致用 如图,一根电线杆在离地面 6 米处断裂,电线杆顶部落在离电线杆底部 8 米处,电线杆折断之前有多高?1.求下列图中表示边的未知数 x、y、z 的值.面积正方形 A正方形 B正方形 C方格数面积ABC ⑴观察图形并填写:(图中每个小方格代表一个单位面积) ⑴观察图形并填写:(图中每个小方格代表一个单位面积)AB教学环节 4 总结反思