高中数学 递推数列通项公式的求法课件 新人教A版必修5 课件VIP免费

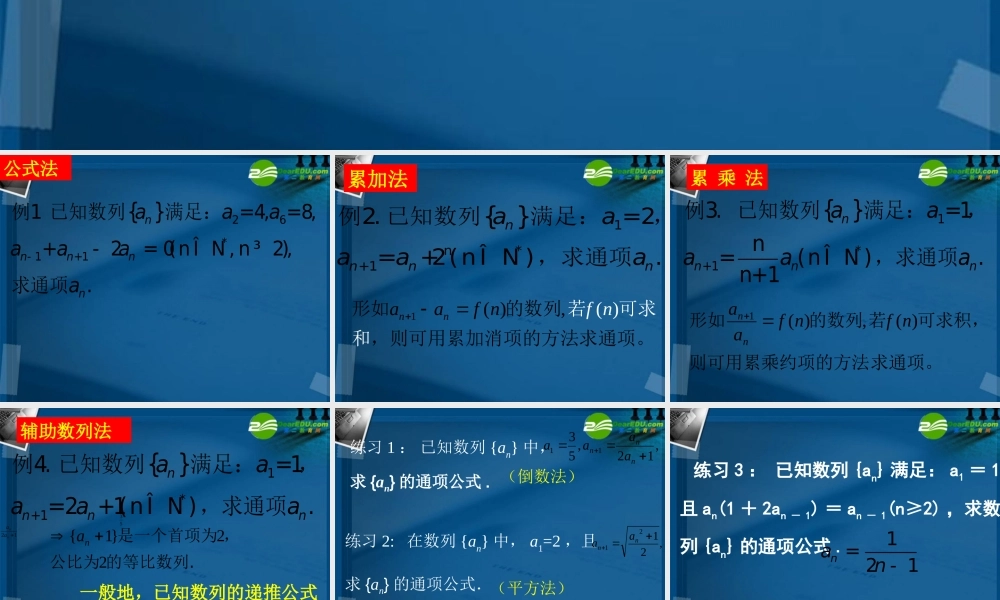
高一数学必修五第二章 《数列》递推数列通项公式的求法 公式法{ }2611=4,=8,+202,.nnnnnaaaaaaa-+ -=γ*例1 已知数列满足：(nN , n)求通项 { }n*例2. 已知数列满足：，+2(nN )，求通项1+1=2=.nnnnaaaaaÎ1((,))nnf naaf n 若可求和形如的数列，则可用累加消项的方法求通项。累加法 { }*例3. 已知数列满足：，(nN )，求通项1+1=1n=.n+1nnnnaaaaaÎ求通项。则可用累乘约项的方法可求积，若的数列形如)(,)(1nfnfaann累 乘 法 { }*例4. 已知数列满足：，(nN )，求通项1+1 =1=2+1.nnnnaaaaaÎ5312nnaa{1}22na 是一个首项为 ，公比为 的等比数列.辅助数列法 一般地，已知数列的递推公式为 an+1=pan+ q, 其中 p,q 为常数 , 求通项公式，可以转化为等比数列求解。 ,12,5311nnnaaaa练习 1 ： 已知数列 {an} 中，求 {an} 的通项公式 . （倒数法）（平方法）练习 2: 在数列 {an} 中， a1=2 ，且求 {an} 的通项公式．,2121nnaa 练习 3 ： 已知数列 {an} 满足： a1 ＝ 1 ，且 an(1 ＋ 2an － 1) ＝ an － 1(n≥2) ，求数列 {an} 的通项公式 .121nan=- 综合分析法{ }*例6. 已知数列满足：nN , n，求通项111= ,220(2).nnnnnaaaS Sa-+=γ1*15,25()1.nnnnanSSSnnNa例5. 已知数列的首项，前 项和为且证明：是等比数列 已知 Sn 与 an 、 n 间的等量关系，求 an 的问题方法 2: 转化为 Sn 的递推关系，先求出 Sn 与 n 之间的关系，再求 an 的通项公式；方法 1 ：利用转化为 an 的递推关系，再求其通项公式；(2)nSSa nnn-1 归纳法不完全归纳猜想证明{ }*例7. 已知数列满足：(nN , n2)，求通项12+1+11 1,,4(1)=n().nnnnnnaaaa aaaa==--γ 第 67 页复习参考题讲解