高一数学 53-1同角三角比的关系和诱导公式课件VIP免费

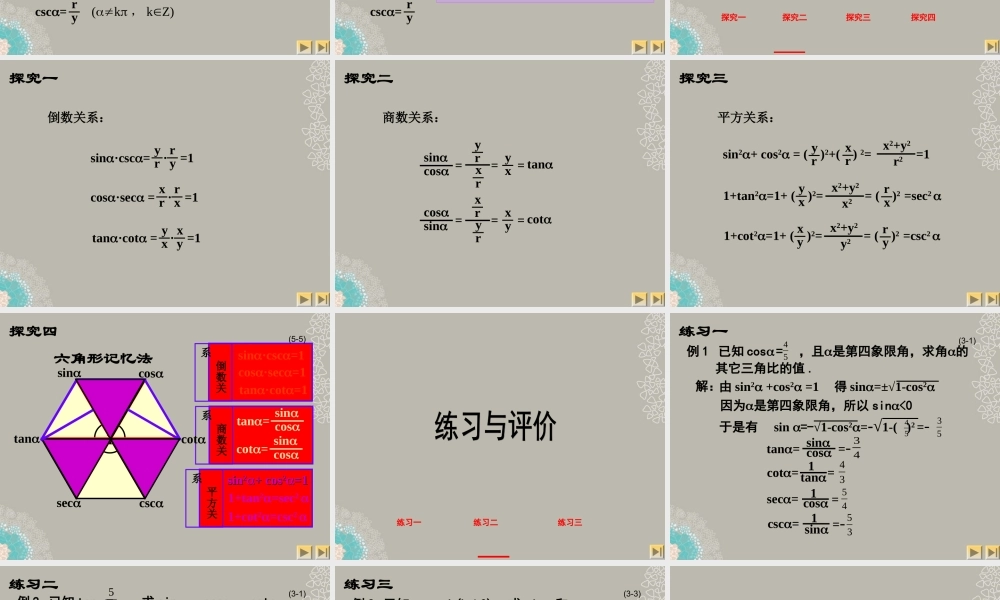
§5.3-1§5.3-1 同角三角比的关系和同角三角比的关系和诱导公式诱导公式The Relationship between Trigonomertic Rations of The Same Angle and The Induction Formulas教学目标学习要求1. 掌握同角三角比的关系的推导过程2. 熟记同角三角比的八个基本关系式3. 已知一个角的一个三角比，能熟练运用同角 三角比的关系求这个角的其它三角比的值。目标与要求导入一导入二(R)任意角三角比的定义 知识回顾：oyxP(x,y)·OP=rsin= yrcos= xrcot= xysec= rxcsc= ry tan= yx(R)(k ， kZ)(k ， kZ)(k+ ， kZ)2(k+ ， kZ)2r2=x2+y2准备与导入一任意角三角比的定义 知识回顾：准备与导入二 这六个三角比中，每一个三角比都是 x 、 y 、 r 三个量中的两个的有序比，并且 r2 = x2 +y2 ，这说明它们相互之间一定存在着某种联系，请同学们仔细观察、比较、分析，你能发现它们之间的联系吗？sin= yrcos= xrcot= xysec= rxcsc= ry tan= yx探究一探究二探究三探究四sin·csc= · =1ryyrcos·sec = · =1rxxrtan·cot = · =1xyyx倒数关系：探究一= = =cosxrsinyr cotxysinyrcosxr tanyx= = =商数关系：探究二sin2+ cos2 = ( )2+( ) 2= =1yrxrr2x2+y2 1+tan2=1+ ( )2= = ( )2 =sec2 rxyxx2x2+y2 1+cot2=1+ ( )2= = ( )2 =csc2 ryxyy2x2+y2平方关系：探究三 商数关系 倒数关系 平方关系1sincostancotseccscsin·csc=1cos·sec=1tan·cot=1sincostan=sincoscot=sinsin22+ cos+ cos22=1=11+tan2=sec2 1+cot2=csc2 六角形记忆法(5-5)探究四练习一练习二练习三例 1 已知 cos = ，且是第四象限角，求角的 其它三角比的值 .45解：由 sin2 +cos2 =1得 sin=±√1-cos2因为是第四象限角，所以 sin<0于是有 sin =-√1-cos2=-√1-( )2 =-4535sincostan= =-34cot= = 1 tan43 1cossec==54 1sincsc==- 53练习一(3-1)例 2 已知 tan = ，求 sin 、 cos 、 cot.512解： 1 tancot==125 1+tan2=sec2 = 1cos2 又 tan = 512∴  是第一象限角或第三象限角当 是第一象限角时，有 sin>0 ， cos>...