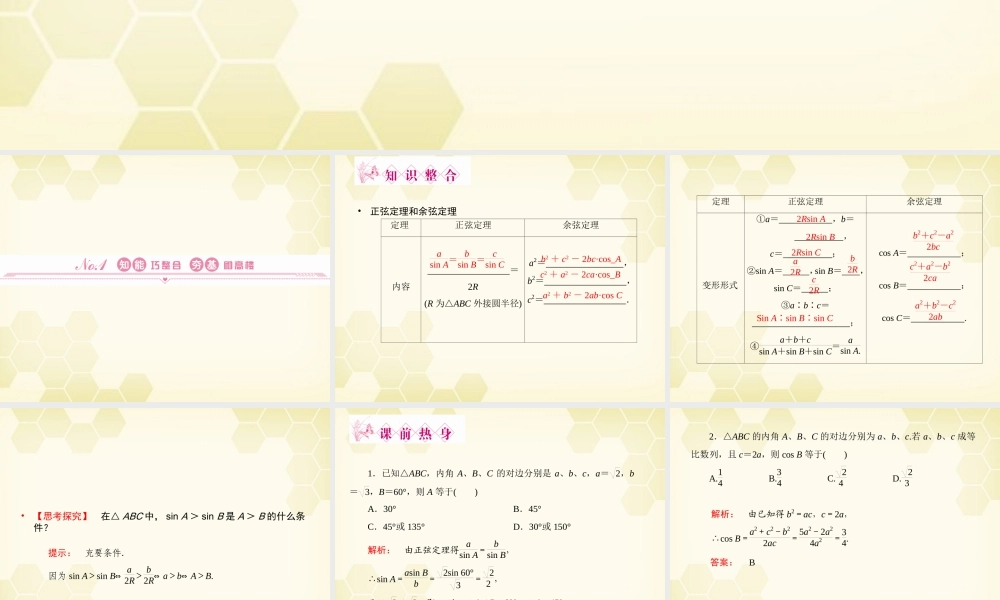
• 第 7 课时 正弦定理和余弦定理 •正弦定理和余弦定理 定理 正弦定理 余弦定理 内容 =2R (R 为△ABC 外接圆半径) a2= , b2= , c2= . asin A= bsin B= csin C b2 + c2 - 2bc·cos_A c2 + a2 - 2ca·cos_B a2 + b2 - 2ab·cos C 定理 正弦定理 余弦定理 变形形式 ①a= ,b= , c= ; ②sin A= ,sin B= , sin C= ; ③a∶b∶c= ; ④a+b+csin A+sin B+sin C=asin A. cos A= ; cos B= ; cos C= . 2Rsin A 2Rsin B 2Rsin C a2R b2R c2R Sin A∶sin B∶sin C b2+c2-a22bc c2+a2-b22ca a2+b2-c22ab •【思考探究】 在△ ABC 中, sin A > sin B 是 A > B 的什么条件?提示: 充要条件. 因为 sin A>sin B⇔ a2R> b2R⇔ a>b⇔ A>B. 1.已知△ABC,内角 A、B、C 的对边分别是 a、b、c,a= 2,b= 3,B=60°,则 A 等于( ) A.30° B.45° C.45°或 135° D.30°或 150° 解析: 由正弦定理得 asin A= bsin B, ∴sin A=asin Bb= 2sin 60°3= 22 , 又 2< 3,即 a<b,∴A<B=60°,∴A=45°. 答案: B 2.△ABC 的内角 A、B、C 的对边分别为 a、b、c.若 a、b、c 成等比数列,且 c=2a,则 cos B 等于( ) A.14 B.34 C. 24 D. 23 解析: 由已知得 b2=ac,c=2a, ∴cos B=a2+c2-b22ac=5a2-2a24a2=34. 答案: B 3.在△ABC 中,若 tan A=34,C=120°,BC=2 3,则 AB=( ) A.3 B.4 C.5 D.6 解析: 因为 tan A=34,所以 sin A=35,由正弦定理 ABsin C= BCsin A,可得 AB=BC·sin Csin A =2 3× 3235=5. 答案: C 4.在△ABC 中,如果 A=60°,c= 2,a= 6,则△ABC 的形状是________. 解析: 由正弦定理 asin A= csin C, ∴sin C=12 ∴C=30°(a>c,C 只能是锐角). 答案: 直角三角形 5.在△ABC 中,如果 A=60°,c=4,a= 6,则三角形解的情况是________. 解析: csin A=4sin 60°=2 3> 6,∴三角形无解. 答案: 无解 •1 .利用正弦定理可解决以下两类三角形:一是已知两角和一角的对边,求其他边角;二是已知两边和一边的对角,求其他边角.•2 .利用余弦定理可解两类三角形:一是已知两边和它们的夹...