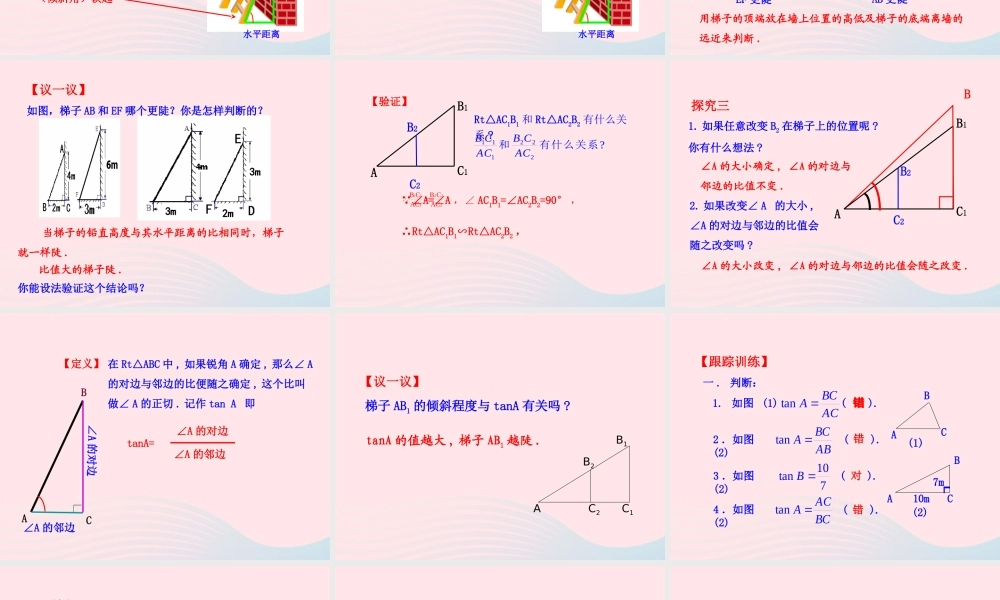
第一章 直角三角形的边角关系1 从梯子的倾斜程度谈起第 1 课时 1. 经历探索直角三角形中边角关系的过程 .理解正切的意义和与现实生活的联系 .2. 能够用 tan A 表示直角三角形中两边的比,表示生活中物体的倾斜程度、坡度等,能够用正切进行简单的计算 . 梯子、地面与墙之间形成一个直角三角形,梯子的铅直高度及梯子的水平距离可以看做是它的直角边,梯子的长可以看做是斜边 .铅直高度水平距离 研究直角三角形的边与角的关系,让我们就从梯子与地面的夹角(倾斜角)谈起【议一议】探究一 梯子在上升变陡的过程中,倾斜角的大小发生了什么变化?倾斜角越大——梯子越陡铅直高度水平距离用梯子的顶端放在墙上位置的高低及梯子的底端离墙的远近来判断 .探究二如图,梯子 AB 和 EF 哪个更陡?你是怎样判断的?EF 更陡AB 更陡3m3m2m【议一议】如图,梯子 AB 和 EF 哪个更陡?你是怎样判断的? 当梯子的铅直高度与其水平距离的比相同时,梯子就一样陡 .比值大的梯子陡 .你能设法验证这个结论吗?AB1C1C2B2112212B CB C .ACAC ∠A=∠A ,∠ AC1B1=∠AC2B2=90° ,∴Rt△AC1B1∽Rt△AC2B2 ,Rt△AC1B1 和 Rt△AC2B2 有什么关系 ??222111有什么关系和 ACCBACCB【验证】C2AB1C1B2B1. 如果任意改变 B2 在梯子上的位置呢 ?你有什么想法 ?∠A 的大小确定 , ∠A 的对边与邻边的比值不变 .2. 如果改变∠ A 的大小 , ∠A 的对边与邻边的比值会随之改变吗 ?∠A 的大小改变 , ∠A 的对边与邻边的比值会随之改变 .探究三在 Rt△ABC 中 , 如果锐角 A 确定 , 那么∠ A的对边与邻边的比便随之确定 , 这个比叫做∠ A 的正切 . 记作 tan A 即BAC∠A 的邻边∠A 的对边tanA=∠A 的对边∠A 的邻边【定义】梯子 AB1 的倾斜程度与 tanA 有关吗 ?tanA 的值越大 , 梯子 AB1 越陡 .AB1C2C1B2【议一议】一 . 判断:ABC(1)┍ABC7m10m(2)4 .如图 (2) ( ). BCACA tan2 .如图 (2) ( ). ABBCA tan3 .如图 (2) ( ). 710tanB1. 如图 (1)( ). ACBCA tan错对错错【跟踪训练】二 . 填空 :1. 如图, tan = tan = 2. 如图 , ∠ACB=90°,CD⊥AB. tan∠ACD=_____ ┌ACBDABCACBC,BC .ACCDADACBCBAtan B =_____=_____CDBD例 1 :下图表示甲、乙两个自动扶梯 , 哪一个自动扶梯比较陡 ?【解析】甲梯中 ,β5m┌13m6m┐8m α乙梯...