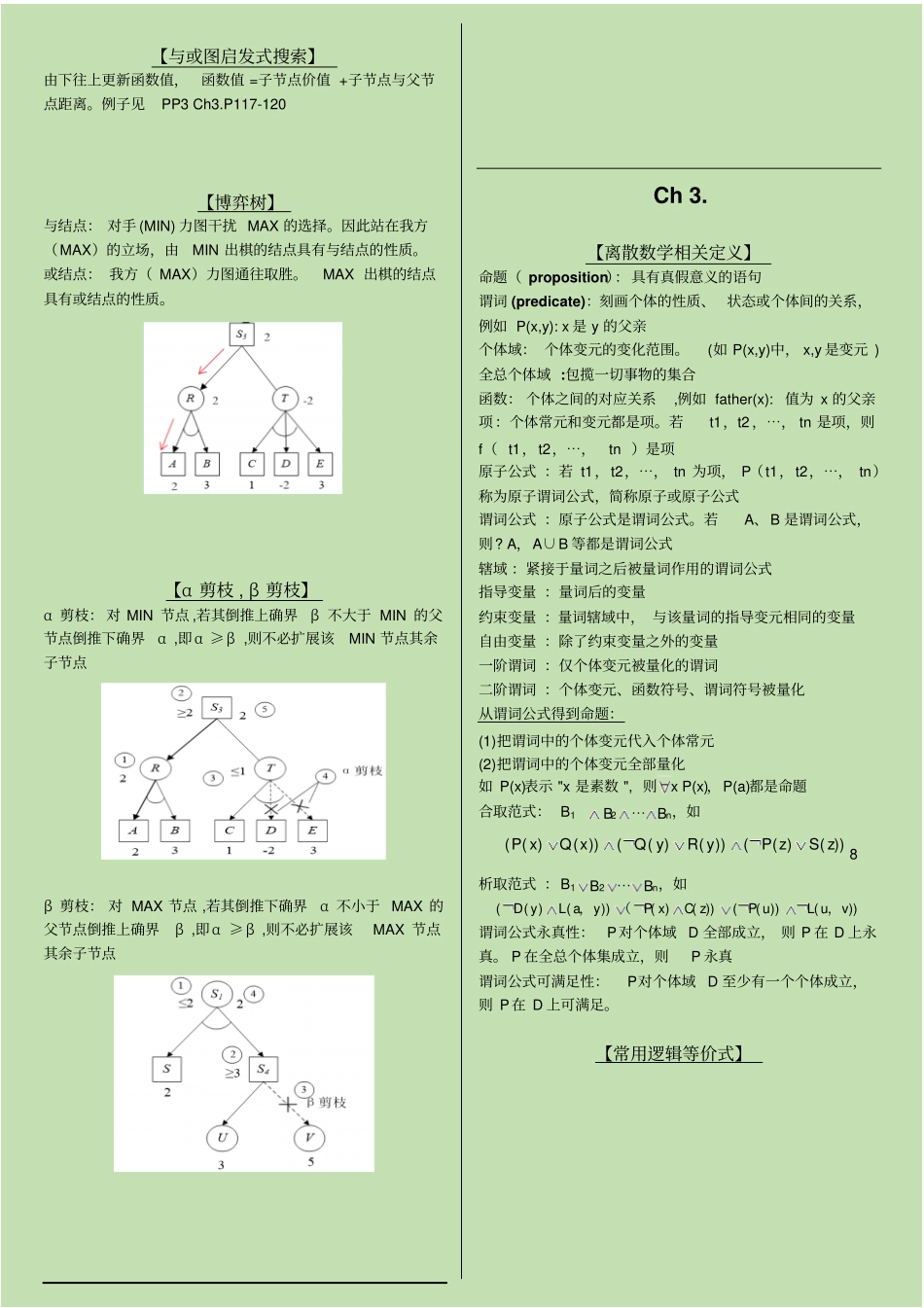
华南理工大学《人工智能》复习资料Ch 2. 【状态空间表示】SFG, ,S:初始状态的集合F:操作的集合G:目标状态的集合例如:507{}{}{}QabcQQ,, ,, ,【状态空间图】【状态空间图搜索使用的数据结构】OPEN表:已生成但没考察的节点(待考察节点 ) CLOSED表 :考察过的节点及节点间关系(搜索树 ) 【广度 / 深度优先搜索特点】广度优先 :完备的 (一定能找到最优解),搜索效率低, OPEN表为队列结构深度优先 :不能保证找到最优解,OPEN表为堆栈结构有界深度优先搜索:即使能求出解,也不一定是最优可变界深度优先搜索算法:深度可变, 每次深度超过阈值的点,都被当作待考察点(在 CLOSED表中 ) 【启发式搜索算法分类】按选择范围分类:全局择优搜索 :考虑所有待考察节点局部择优搜索 :只考虑当前节点的子节点【A*算法】f( x) =g(x)+ h(x)g(x)为当前点的代价h(x)为距离目标的距离A*对 A 算法的改进:对 h(x)作限制,使其总是小于实际最小距离h(x) h* (x),具有完备性【与或图】Q 与 Q1,Q2 与等价 (即 Q 可以分解为Q1+Q2)Q1 与{Q1i},{Q1i’}或等价 (即 Q1 可以转换为 {Q1i}或{Q1i ’})【与或图中的概念】本原问题 :直接可解的问题。终止节点 :本原问题对应的节点端节点 :无子节点的节点与节点 :子节点为与关系或节点 :子节点为或关系【与或图的广度 / 深度搜索】Step1:S0 放入 OPEN表Step2:OPEN表第一个点(记为N)取出放入CLOSED表,冠以编号 n。Step3:若 n 可扩展:(1)扩展 N,其子节点放入OPEN表(深度 :尾部,广度 :首部 ) (2)考查这些节点是否终止节点。若是,放入CLOSED表,标为可解节点, 并对先辈点标示。若S0被标可解, 得解。(3)从 OPEN表删除具有可解先辈的节点。转Step2。Step4:若 N 不可扩展:(1)标示 N 为不可解。(2)标示先辈节。若S0被标不可解,失败。(3)从 OPEN表删除具有不可解先辈的节点。转Step2。【与或图启发式搜索】由下往上更新函数值,函数值 =子节点价值 +子节点与父节点距离。例子见PP3 Ch3.P117-120 【博弈树】与结点: 对手 (MIN) 力图干扰 MAX 的选择。因此站在我方(MAX)的立场,由MIN 出棋的结点具有与结点的性质。或结点: 我方( MAX)力图通往取胜。MAX 出棋的结点具有或结点的性质。【α 剪枝 , β 剪枝】α 剪枝: 对 MIN 节点 ,若其倒推上确界β 不大于 MIN 的父节点倒推下确界α ,即...