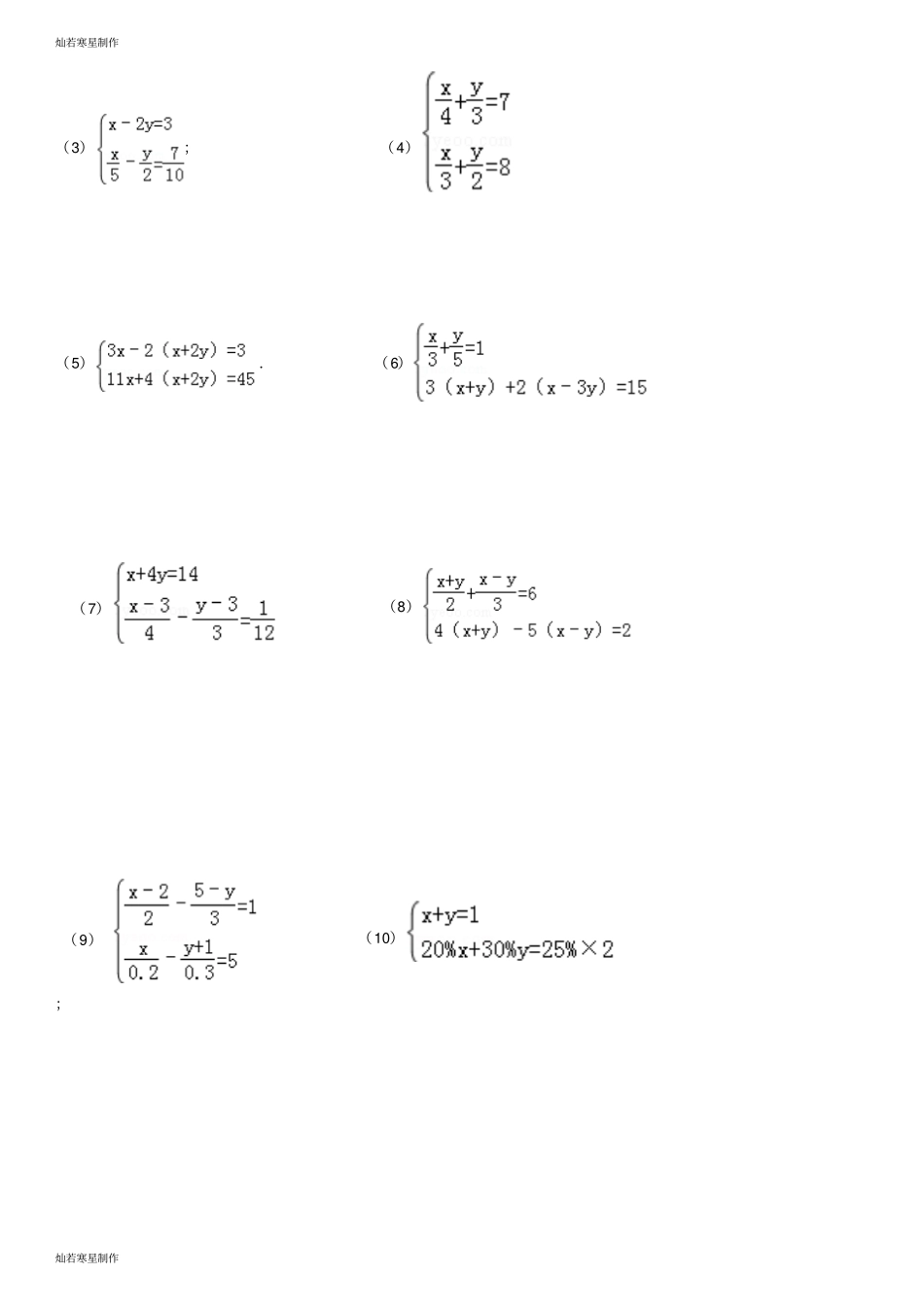
灿若寒星制作灿若寒星制作二元一次方程组解法练习题一.解答题(共16 小题)1.解下列方程组(1)(2)(3))(6441125为已知数aayxayx(4)(5)(6).(7)(8)0)1(2)1()1(2xyxxxyyx(9)(10)1213222132yxyx灿若寒星制作灿若寒星制作2.求适合的 x,y 的值.3.已知关于x,y 的二元一次方程y=kx+b 的解有和.(1)求 k,b 的值.(2)当 x=2 时, y 的值.(3)当 x 为何值时, y=3 ?1.解下列方程组(1)( 2);灿若寒星制作灿若寒星制作(3);(4)(5).(6)(7)(8)(9)(10);灿若寒星制作灿若寒星制作2.在解方程组时,由于粗心,甲看错了方程组中的a,而得解为,乙看错了方程组中的 b,而得解为.(1)甲把 a 看成了什么,乙把b 看成了什么?(2)求出原方程组的正确解.灿若寒星制作灿若寒星制作二元一次方程组解法练习题精选参考答案与试题解析一.解答题(共16 小题)1.求适合的 x,y 的值.考点 : 解二元一次方程组.分析:先把两方程变形(去分母),得到一组新的方程,然后在用加减消元法消去未知数x,求出 y 的值,继而求出x 的值.解答:解:由题意得:,由( 1)×2 得: 3x﹣2y=2 (3),由( 2)×3 得: 6x+y=3 (4),( 3)×2 得: 6x﹣4y=4(5),( 5)﹣( 4)得: y=﹣,把 y 的值代入( 3)得: x=,∴.点评:本题考查了二元一次方程组的解法,主要运用了加减消元法和代入法.2.解下列方程组(1)(2)(3)(4).考点 : 解二元一次方程组.分析:( 1)(2)用代入消元法或加减消元法均可;( 3)(4)应先去分母、去括号化简方程组,再进一步采用适宜的方法求解.解答:解:(1)① ﹣ ② 得,﹣ x=﹣2,解得 x=2 ,把 x=2 代入 ① 得, 2+y=1 ,解得 y=﹣1.故原方程组的解为.( 2)①×3﹣②×2 得,﹣ 13y= ﹣39,解得, y=3,灿若寒星制作灿若寒星制作把 y=3 代入 ① 得, 2x﹣3×3=﹣5,解得 x=2 .故原方程组的解为.( 3)原方程组可化为,① +② 得, 6x=36,x=6 ,① ﹣② 得, 8y=﹣4,y= ﹣.所以原方程组的解为.( 4)原方程组可化为:,①×2+② 得, x=,把 x=代入 ② 得, 3× ﹣4y=6,y= ﹣.所以原方程组的解为.点评:利用消元法解方程组,要根据未知数的系数特点选择代入法还是加减法:① 相同未知数的系数相同或互为相反数时,宜用加减法;② 其中一个未知数的系数为1 ...