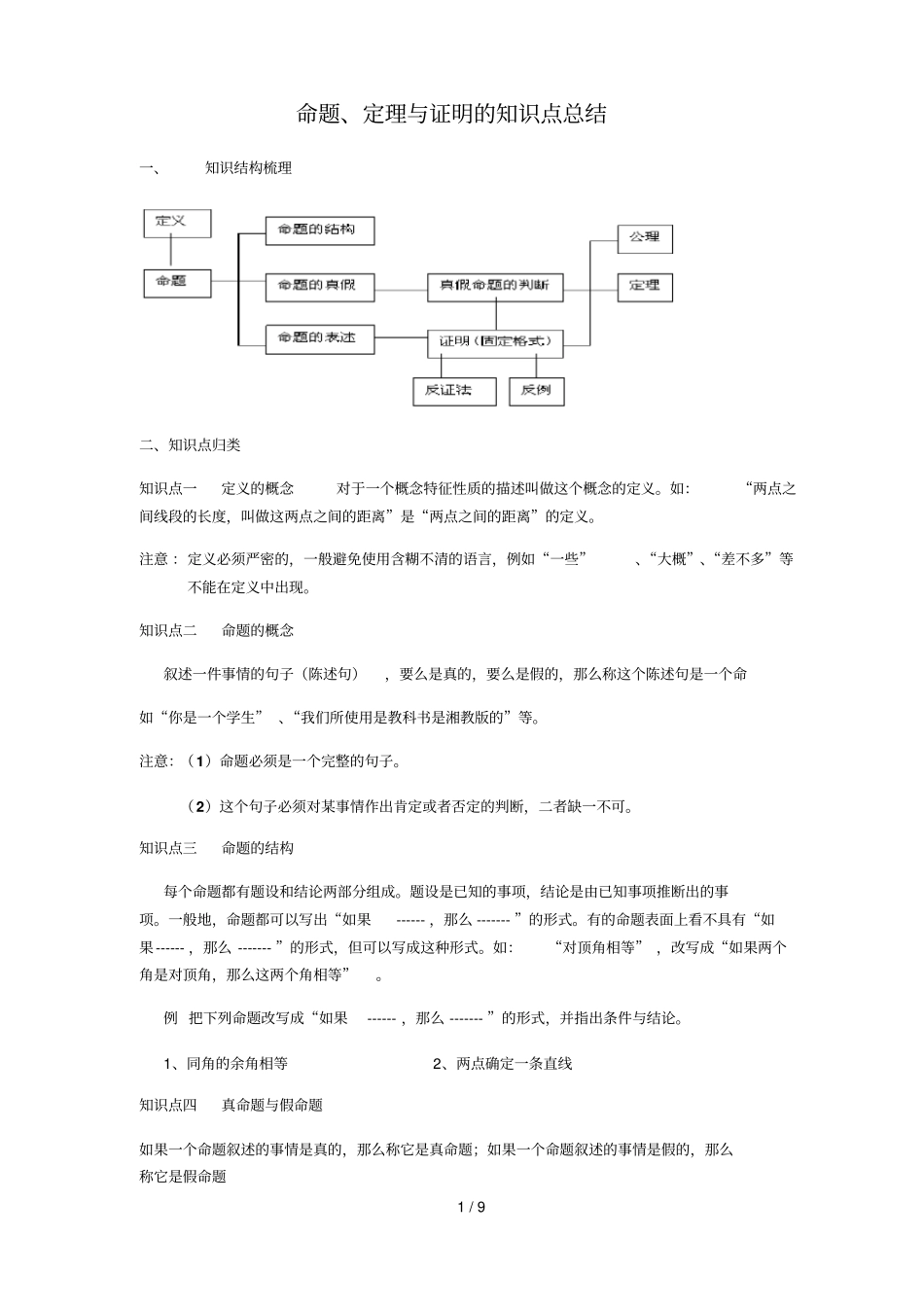
1 / 9 命题、定理与证明的知识点总结一、知识结构梳理二、知识点归类知识点一定义的概念对于一个概念特征性质的描述叫做这个概念的定义。如:“两点之间线段的长度,叫做这两点之间的距离”是“两点之间的距离”的定义。注意 :定义必须严密的,一般避免使用含糊不清的语言,例如“一些”、“大概”、“差不多”等不能在定义中出现。知识点二命题的概念叙述一件事情的句子(陈述句),要么是真的,要么是假的,那么称这个陈述句是一个命如“你是一个学生” 、“我们所使用是教科书是湘教版的”等。注意:(1)命题必须是一个完整的句子。(2)这个句子必须对某事情作出肯定或者否定的判断,二者缺一不可。知识点三命题的结构每个命题都有题设和结论两部分组成。题设是已知的事项,结论是由已知事项推断出的事项。一般地,命题都可以写出“如果------ ,那么 ------- ”的形式。有的命题表面上看不具有“如果------ ,那么 ------- ”的形式,但可以写成这种形式。如:“对顶角相等” ,改写成“如果两个角是对顶角,那么这两个角相等”。例 把下列命题改写成“如果------ ,那么 ------- ”的形式,并指出条件与结论。1、同角的余角相等2、两点确定一条直线知识点四真命题与假命题如果一个命题叙述的事情是真的,那么称它是真命题;如果一个命题叙述的事情是假的,那么称它是假命题2 / 9 注意:真、假命题的区别就在于其是否是正确的,在判断命题的真假时,要注意把握这点。知识点五证明及互逆命题的定义1、 从一个命题的条件出发,通过讲道理(推理),得出它的结论成立,这个过程叫作证明。注意:证明一个命题是假命题的方法是举反例,即找出一个例子,它符合命题条件,但它不满足命题的结论,从而判断这个命题是假命题。2、 一个命题的条件和结论分别是另一个命题的结论和条件,这两个命题称为互逆的命题,其中的一个命题叫作另一个命题的逆命题。注意 :一个命题为真不能保证它的逆命题为真,逆命题是否为真,需要具体问题具体分析。例 说出下列命题的逆命题,并指出它们的真假。(1)直角三角形的两锐角互余;(2)全等三角形的对应角相等。类型一:例、判断下列语句在表述形式上,哪些对事情作了判断?哪些没有对事情作出判断?(1)对顶角相等;(2)画一个角等于已知角;(3)两直线平行,同位角相等;(4), 两条直线平行吗? (5)鸟是动物;(6)若,求的值; (7)若,则.思路点拨 :通过本题熟悉命题的定义解析: ...