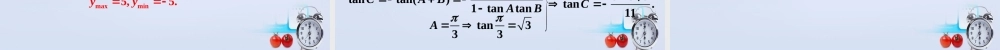数学 3.2两角和与差的三角函数(第3课时)教学课件 北师大版必修4 课件VIP免费

复习回顾1. 两角和与差的正、余弦公式：CcoscoscossinsinSsinsincoscossin2. 两角和与差的正切公式：tan(tantan()1tanta)nT 3. 两角和与差的正、余弦、正切公式的灵活运用：（ 1 ）公式的正用、逆用、变形运用；（ 2 ）角的变换、单角化复角、复角化单角的变形运用 .§2 两角和与差的三角函数（三）1. 三角恒等式证明例 1. 求证：2222sin()sin()tan1sincostan 证明：左边 =22(sincoscossin)(sincoscossin)sincos222222sincoscossinsincos2222cossin1sincos 22tan1tan = 右边∴ 等式成立 .练习 1. 求证：2222tantan(1)tan()tan();1tantanxyxyxyxy 55(2)sin()sin()cos .66归纳：在三角恒等变形时，要注意（ 1 ）角的变形，如拆角或并角；（ 2 ）公式的正用、逆用及变形运用 .例 2. 求证：ABBABAAsin(2)sin- 2cos()sinsin证明：左边 = []sin- 2cos()sin()sinABAABAAsin()coscos()sin2cos()sinsinABAABAABAAsin()coscos()sinsinABAABAAsin[()]sinABAAsinsinBA= 右边∴ 等式成立 .例 3. 求证：cos3 sin2sin()6证明：左边 =132( cossin)222(sincoscossin)662sin()6= 右边 ∴ 等式成立 .练习 2. 填空：13(1)cossin__________________;22(2)sincos____________________;xxxx(3)sincos____________________;26(4)sin()cos()__________________________;4444xxsin()6cos()32 sin(-)4x 2 cos()4x－2 sin()4x2 cos()4x 122 cos()2x -25sin()212x 22sincossin()abab 由 确定 , 称为辅助角 .2222sincosbabaabsincosab2. 形如 的三角函数化简练习 3. 求函数 的最大值和最小值 .3sin4cosyxxmaxmin5,5.yy练习 4. 已知 A 、 B 、 C 是△ ABC 的三内角，向量 且(cos,sin),nAA( 1,3),m  1.m n （ 1 ）求∠ A;（ 2 ）若 求2212sincos3,cossinBBBBtan.C解：（ 1 ）131AA m nsincos即162Asin()50666AA   66A3A.（ 2 ）BBBBBBBB2222212sincos(cossin)33cossincossinABCABABtantantantan()1tantanBBsin2cosBtan2C 85 3tan.11A tan3333. 小 结（ 1 ）三角恒等式证明 ;absincos（ 2 ）形如 的三角函数化简 ;22sincossin()abab 由 确定 , 称为辅助角 .2222sincosbabaab