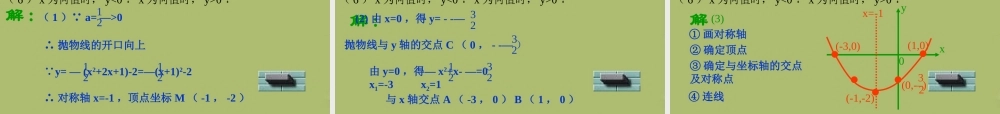二次函数复习退出一、定义二、顶点与对称轴三、关系式的求法四、图象位置与a 、 b 、 c 、 的正负关系一、定义二、顶点与对称轴四、图象位置与a 、 b 、 c 、 的正负关系一般地,如果 y=ax2+bx+c(a , b , c 是常数, a≠0) ,那么, y叫做 x 的二次函数。三、关系式的求法一、定义二、顶点与对称轴三、关系式的求法四、图象位置与a 、 b 、 c 、 的正负关系y=ax2+bx+cy=a(x+ )2+ b2a4ac-b24a 对称轴: x= – b2a顶点坐标:(– ,) b2a4ac-b24a一、定义二、顶点与对称轴三、关系式的求法四、图象位置与a 、 b 、 c 、 的正负关系 关系式使用范围一般式已知任意三个点顶点式已知顶点( -h,k)及另一点交点式已知与 x轴的两个交点及另一个点y=ax2+bx+cy=a(x+h)2+ky=a(x-x1)(x-x2) (1)a 确定抛物线的开口方向:a>0a<0 (2)c 确定抛物线与 y 轴的交点位置 :c>0c=0c<0 (3)a 、 b 确定对称轴 的位置 :ab>0ab=0ab<0 (4)Δ 确定抛物线与 x 轴的交点个数:Δ>0Δ=0Δ<0x=- b2a (1)a 确定抛物线的开口方向: (2)c 确定抛物线与 y 轴的交点位置 : (3)a 、 b 确定对称轴 的位置 : (4)Δ 确定抛物线与 x 轴的交点个数:xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0x=- b2a (2)c 确定抛物线与 y 轴的交点位置 :(3)a 、 b 确定对称轴 的位置 : (4)Δ 确定抛物线与 x 轴的交点个数:xy0a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0 (1)a 确定抛物线的开口方向:x=- b2a (1)a 确定抛物线的开口方向: (2)c 确定抛物线与 y 轴的交点位置 : (3)a 、 b 确定对称轴 的位置 : (4)Δ 确定抛物线与 x 轴的交点个数:xy0•(0,c)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0x=- b2a (1)a 确定抛物线的开口方向: (2)c 确定抛物线与 y 轴的交点位置 : (3)a 、 b 确定对称轴 的位置 : (4)Δ 确定抛物线与 x 轴的交点个数:xy0•(0,0)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0x=- b2a (1)a 确定抛物线的开口方向: (2)c 确定抛物线与 y 轴的交点位置 : (3)a 、 b 确定对称轴 的位置 : (4)Δ 确定抛物线与 x 轴的交点个数:xy0•(0,c)a>0a<0c>0c=0c<0ab>0ab=0ab<0Δ>0Δ=0Δ<0x=- b2a (1)a 确定抛物线的开口方向: (2)c 确定抛物线与 y 轴的交点位置 : (3)a 、 b 确定对称轴 的位置 : (4)Δ 确定抛物线与...