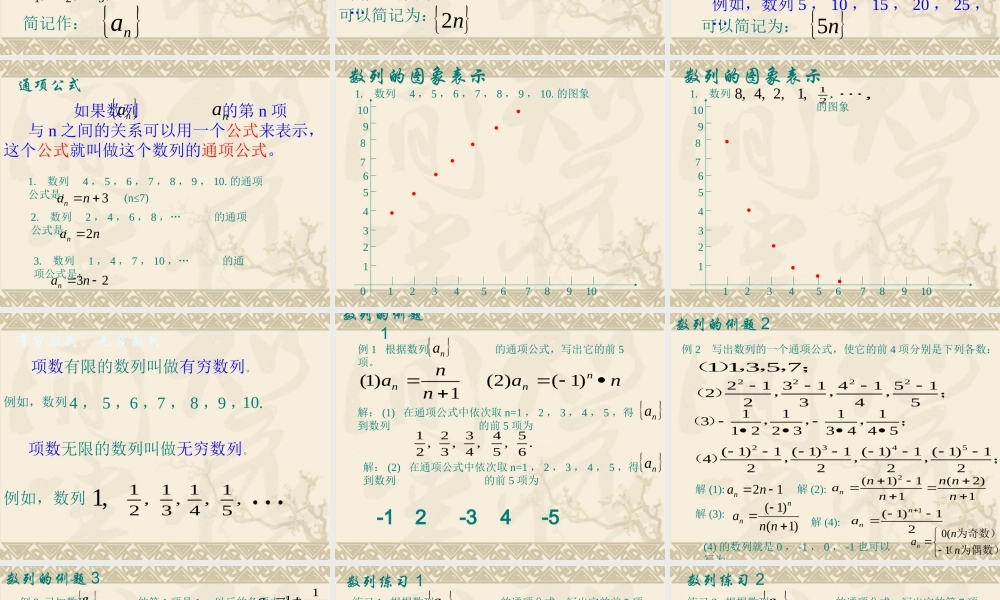
数列学习目标: 通过日常生活中的实例,了解数列的概念和几种简单的表示方法(列表、图象、通项公式),了解数列是一种特殊函数。4 ,5 ,6 ,7 ,8 ,9 ,10.堆放的钢管正整数的倒数:的值:,精确到,001.0,01.0,1.0121,1 ,21 ,31 ,41 ,51 ,1.4 ,1.41 ,1.414 ,… ,-1 的 1 次幂, 2 次幂, 3 次幂, 4 次幂,…排成的一列数:-1 ,1 ,-1 ,1 ,-1 ,1 ,…无穷多个 1 排成的一列数:1 , 1 , 1 , 1 , 1 , 1 ,…数列的定义按一定的次序排列的一列数叫做数列。数列中的每一个数叫做这个数列的项。数列中的各项依次叫做这个数列的第 1 项(或首项)用 表示,1a第 2 项用 表示,2a… ,第 n 项用 表示,na… ,数列的一般形式可以写成:,1a,2a,3a,na… ,… ,简记作: na通项公式例如,数列,1,21,31,41,51可以简记为:n1例如,数列 1 , 2 , 3 , 4 , 5 , 6 ,…可以简记为: n例如,数列 2 , 4 , 6 , 8 , 10 , 12 ,…可以简记为:n2通项公式例如,数列 1 , 3 , 5 , 7 , 9 , 11 ,…可以简记为:12 n例如,数列 1 , 10 , 100 , 1000 ,…可以简记为: 110 n例如,数列 1 , -1 , 1 , -1 , 1 , -1 ,…可以简记为: 1)1(n例如,数列 5 , 10 , 15 , 20 , 25 ,…可以简记为: n5通项公式 如果数列 的第 n 项 与 n 之间的关系可以用一个公式来表示,这个公式就叫做这个数列的通项公式。 nana1. 数列 4 , 5 , 6 , 7 , 8 , 9 , 10. 的通项公式是:3nan(n≤7)2. 数列 2 , 4 , 6 , 8 ,… 的通项公式是:nan23. 数列 1 , 4 , 7 , 10 ,… 的通项公式是:23 nan数列的图象表示1. 数列 4 , 5 , 6 , 7 , 8 , 9 , 10. 的图象1234567891012345678910●●●●●●●0数列的图象表示1. 数列 的图象1234567891012345678910,8,4,2,1,21,●●●●●●有穷数列、无穷数列项数有限的数列叫做有穷数列。项数无限的数列叫做无穷数列。例如,数列,1,21,31,41,514 , 5 ,6 ,7 , 8 ,9 ,10.例如,数列数列的例题1例 1 根据数列 的通项公式,写出它的前 5项。 na1)1(nnannann)1()2(解: (1) 在...