圆锥曲线方程小结 人教版 课件VIP免费

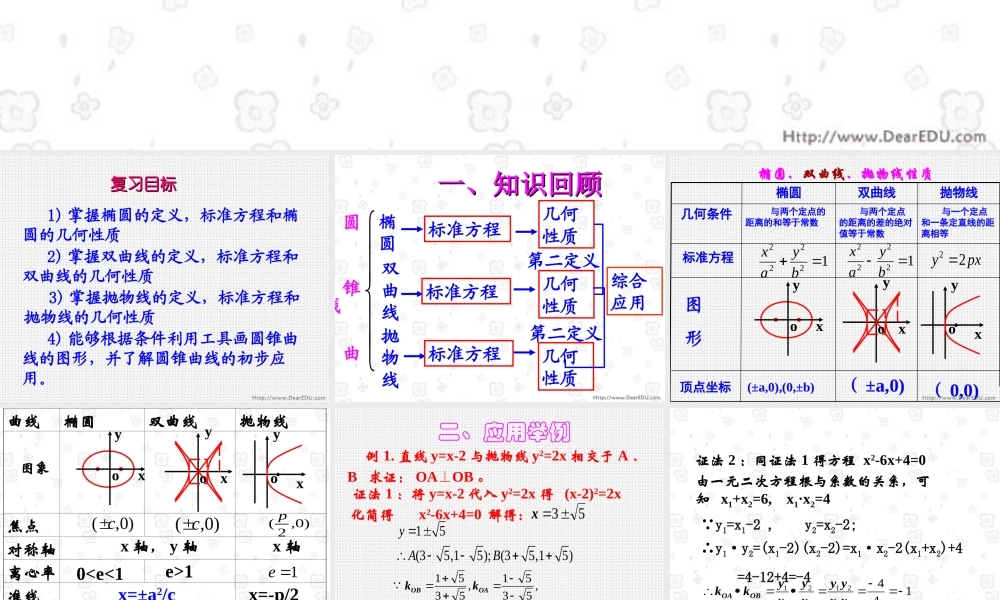
圆锥曲线方程小结复习目标复习目标 1) 掌握椭圆的定义，标准方程和椭圆的几何性质 2) 掌握双曲线的定义，标准方程和双曲线的几何性质 3) 掌握抛物线的定义，标准方程和抛物线的几何性质 4) 能够根据条件利用工具画圆锥曲线的图形，并了解圆锥曲线的初步应用。一、知识回顾一、知识回顾 圆 锥 曲 线椭圆双曲线抛物线标准方程几何性质标准方程几何性质标准方程几何性质第二定义第二定义综合应用 与一个定点和一条定直线的距离相等 与两个定点的距离的差的绝对值等于常数 与两个定点的距离的和等于常数 几何条件抛物线双曲线椭圆12222 byax12222 byaxpxy22 椭圆、双曲线、抛物线性质yxooxyoxy图形(±a,0),(0,±b)（ ±a,0)（ 0,0)顶点坐标标准方程曲线椭圆双曲线抛物线 焦点对称轴离心率准线 渐近线焦半径图象)0,( c)0,( c)0,2( p1e0exar||0aexr2/0pxrx 轴， y 轴x 轴yxooxyoxy 01x=±a2/cx=-p/2y=±(b/a)x 例 1. 直线 y=x-2 与抛物线 y2=2x 相交于 A 、B 求证： OAOB⊥。 证法 1 ：将 y=x-2 代入 y2=2x 得 (x-2)2=2x化简得 x2-6x+4=0 解得：53x15(35,15); (35,15)yAB ,5351,5351OAOBkk1595153515351OAOBkk∴OAOB⊥二、应用举例证法 2 ：同证法 1 得方程 x2-6x+4=0由一元二次方程根与系数的关系，可知 x1+x2=6, x1·x2=4 ∴OAOB⊥ y1=x1-2 , y2=x2-2;∴y1·y2=(x1-2)(x2-2)=x1·x2-2(x1+x2)+4 =4-12+4=-414421212211xxyyxyxykkOBOA 例 2. 一圆与圆 x2+y2+6x+5=0 外切，同时与圆 x2+y2-6x-91=0 内切，求动圆圆心的轨迹方程，并说明它是什么样的曲线解法 1 ：如图：设动圆圆心为 P （ x,y), 半径为 R ，两已知圆圆心为 O1 、O2 。分别将两已知圆的方程 x2+y2+6x+5=0 x2+y2-6x-91=0配方，得 （ x+3)2+y2=4 (x-3)2+y2=100当⊙ P 与⊙ O1: (x+3)2+y2=4 外切时，有 |O1P|=R+2 ①当⊙ P 与⊙ O2: (x-3)2+y2=100 内切时，有 |O2P|=10-R ②① 、②式两边分别相加，得 |O1P|+|O2P|=12即12)3()3(2222yxyxO1PXYO2 化简得 3x2+4y2-108=0即可得1273622 yx所以，动圆圆心的轨迹是椭圆，它的长轴、短轴分别为.3612、解法 2 ：同解法 1 得方程12)3()3(2222yxyx即，动圆圆心 P(x,y) 到点 ...