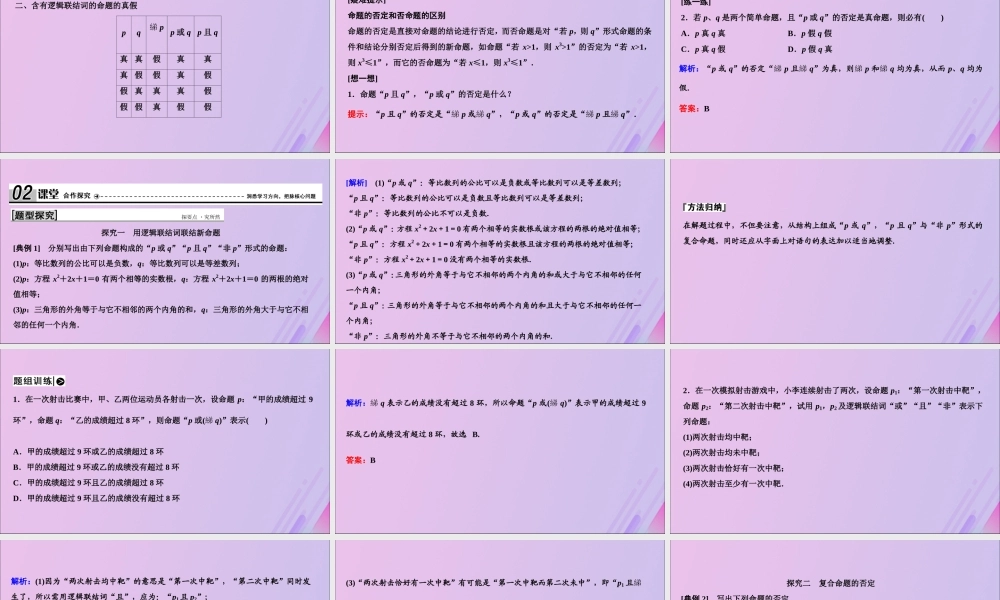
一、用逻辑联结词构成新命题 1.用逻辑联结词“且”联结两个命题 p 和 q,构成一个新命题“ ”. 2.用逻辑联结词“或”联结两个命题 p 和 q,构成一个新命题“ ”. 3.一般地,对命题 p 加以否定,就得到一个新命题,记作 ,读作“ ”. p 且 q p 或 q 綈 p 非 p 二、含有逻辑联结词的命题的真假 p q 綈 p p 或 q p 且 q 真 真 假 真 真 真 假 假 真 假 假 真 真 真 假 假 假 真 假 假 [疑难提示] 命题的否定和否命题的区别 命题的否定是直接对命题的结论进行否定,而否命题是对“若 p,则 q”形式命题的条件和结论分别否定后得到的新命题,如命题“若 x>1,则 x3>1”的否定为“若 x>1,则 x3≤1”,而它的否命题为“若 x≤1,则 x3≤1”. [想一想] 1.命题“p 且 q”,“p 或 q”的否定是什么? 提示:“p 且 q”的否定是“綈 p 或綈 q”,“p 或 q”的否定是“綈 p 且綈 q”. [练一练] 2.若 p、q 是两个简单命题,且“p 或 q”的否定是真命题,则必有( ) A.p 真 q 真 B.p 假 q 假 C.p 真 q 假 D.p 假 q 真 解析:“p 或 q”的否定“綈 p 且綈 q”为真,则綈 p 和綈 q 均为真,从而 p、q 均为假. 答案:B 探究一 用逻辑联结词联结新命题 [典例 1] 分别写出由下列命题构成的“p 或 q”“p 且 q”“非 p”形式的命题: (1)p:等比数列的公比可以是负数,q:等比数列可以是等差数列; (2)p:方程 x2+2x+1=0 有两个相等的实数根,q:方程 x2+2x+1=0 的两根的绝对值相等; (3)p:三角形的外角等于与它不相邻的两个内角的和,q:三角形的外角大于与它不相邻的任何一个内角. [解析] (1)“p 或 q”:等比数列的公比可以是负数或等比数列可以是等差数列; “p 且 q”:等比数列的公比可以是负数且等比数列可以是等差数列; “非 p”:等比数列的公比不可以是负数. (2)“p 或 q”:方程 x2+2x+1=0 有两个相等的实数根或该方程的两根的绝对值相等; “p 且 q”:方程 x2+2x+1=0 有两个相等的实数根且该方程的两根的绝对值相等; “非 p”:方程 x2+2x+1=0 没有两个相等的实数根. (3)“p 或 q”:三角形的外角等于与它不相邻的两个内角的和或大于与它不相邻的任何一个内角; “p 且 q”:三角形的外角等于与它不相邻的两个内角的和且大于与它不相邻的...