八年级数学下册 分式的运算课件 新人教版 课件VIP免费

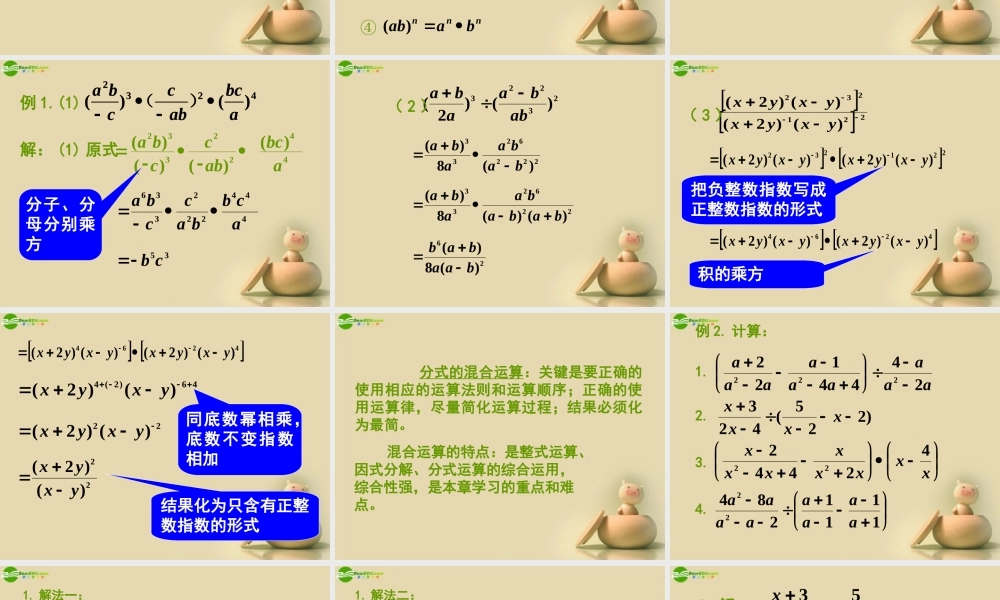
一、提出问题：请问下面的运算过程对吗？32)3(4422xxxxx32)3()2(22xxxx22x二、研究解决： 这是一道关于分式乘除的题目，运算时应注意： 显然此题在运算顺序上出现了错误，除没有转化为乘之前是不能运用结合律的，这一点大家要牢记呦！① 按照运算法则运算；② 乘除运算属于同级运算，应按照先出现的先算的原则，不能交换运算顺序；③ 当除写成乘的形式时，灵活的应用乘法交换律和结合律可起到简化运算的作用；④ 结果必须写成整式或最简分式的形式。正确的解法：32)3(4422xxxxx2)3)(2(2xx除法转化为乘法之后可以运用乘法的交换律和结合律3231)2(22xxxxx三、知识要点与例题解析： 分式的乘方：把分子、分母各自乘方。即 其中 b≠0,a,b 可以代表数，也可以代表代数式。),()(为正整数nbabannn mnnmaa）（③ nnnbaab)( ④nmnmaaa①整数指数幂的运算性质：若 m,n 为整数，且 a≠0,b≠0 ，则有② nmnmaaa23223)()2(abbaaba（ 2 ）221232)()2()()2(yxyxyxyx（ 3 ）例 1.(1) 4232)()(abcabccba）（4232)()(abcabccba）（解： (1) 原式4422332)()()()(abcabccba444222336acbbaccba35cb分子、分母分别乘方例 1.(1) 4232)()(abcabccba）（4232)()(abcabccba）（2226233)(8)(babaaba226233)()(8)(bababaaba26)(8)(baabab23223)()2(abbaaba（ 2 ） 221232)()2()()2(yxyxyxyx 4264)()2()()2(yxyxyxyx把负整数指数写成正整数指数的形式积的乘方221232)()2()()2(yxyxyxyx（ 3 ）46)2(4)()2(yxyx22)()2(yxyx22)()2(yxyx同底数幂相乘，底数不变指数相加结果化为只含有正整数指数的形式 4264)()2()()2(yxyxyxyx 分式的混合运算：关键是要正确的使用相应的运算法则和运算顺序；正确的使用运算律，尽量简化运算过程；结果必须化为最简。 混合运算的特点：是整式运算、因式分解、分式运算的综合运用，综合性强，是本章学习的重点和难点。例 2. 计算：1.2.3.4. aaaaaaaaa2444122222)225(423xxxxxxxxx...