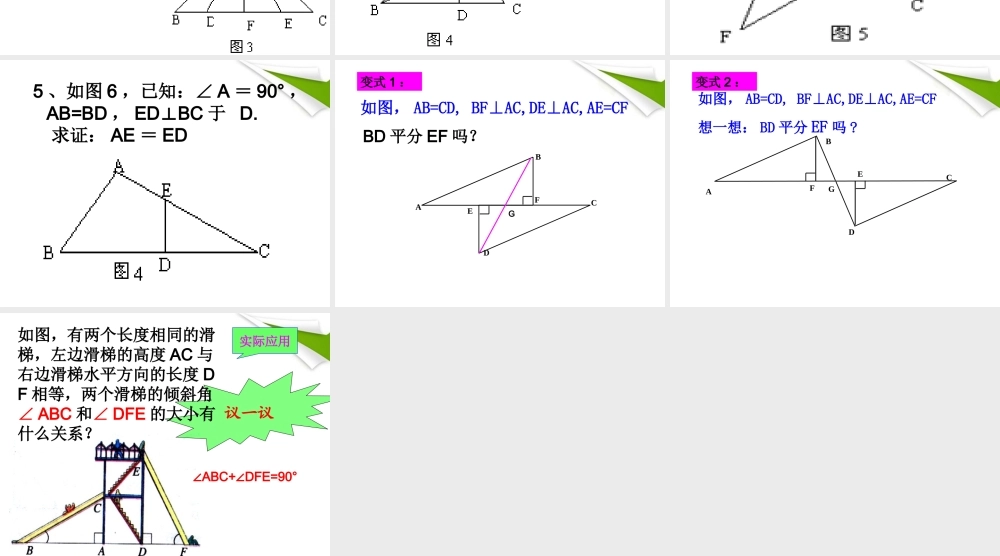
知识回顾:一般三角形 全等的条件:1. 定义(重合)法;2.SSS ;3.SAS ;4.ASA ;5.AAS.直角三角形 全等特有的条件:HL.包括直角三角形不包括其它形状的三角形解题中常用的4 种方法 1. 如图 1 :△ ABF CD≌ △E ,∠ B=30° , ∠ BAE= DCF=20 °.∠求∠ EFC 的度数 .练习题: 2 、如图 3 ,已知:△ ABC 中, DF=FE , BD=CE , AFBC⊥于 F ,则此图中全等三角形共有( ) A 、 5 对 B 、 4 对 C 、 3 对 D 2 对 B 3 、如图 4 ,已知:在△ ABC 中, AD是 BC 边上的高, AD=BD , DE=DC ,延长 BE 交 AC 于 F , 求证: BF 是△ ABC 中边上的高 . 4 、如图 5 ,已知: AB=CD , AD=CB , O 为 AC 任一点,过 O 作直线分别交 AB 、 CD 的延长线于 F 、E ,求证:∠ E= F.∠ 5 、如图 6 ,已知:∠ A = 90° , AB=BD , EDBC⊥于 D. 求证: AE = ED AFCEDB如图, AB=CD, BF⊥AC,DE⊥AC,AE=CF求证: BF=DE变式 1 :BD 平分 EF 吗?G AFCEDB如图, AB=CD, BF⊥AC,DE⊥AC,AE=CF想一想: BD 平分 EF 吗 ?G变式 2 : 议一议如图,有两个长度相同的滑梯,左边滑梯的高度 AC 与右边滑梯水平方向的长度 DF 相等,两个滑梯的倾斜角∠ ABC 和∠ DFE 的大小有什么关系?∠ABC+ DFE=90∠°实际应用