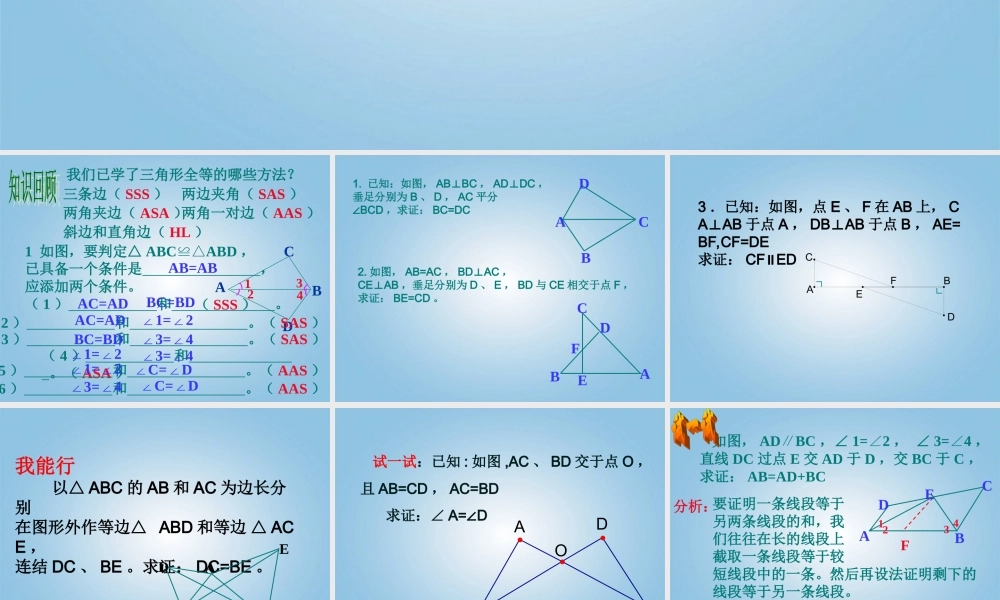
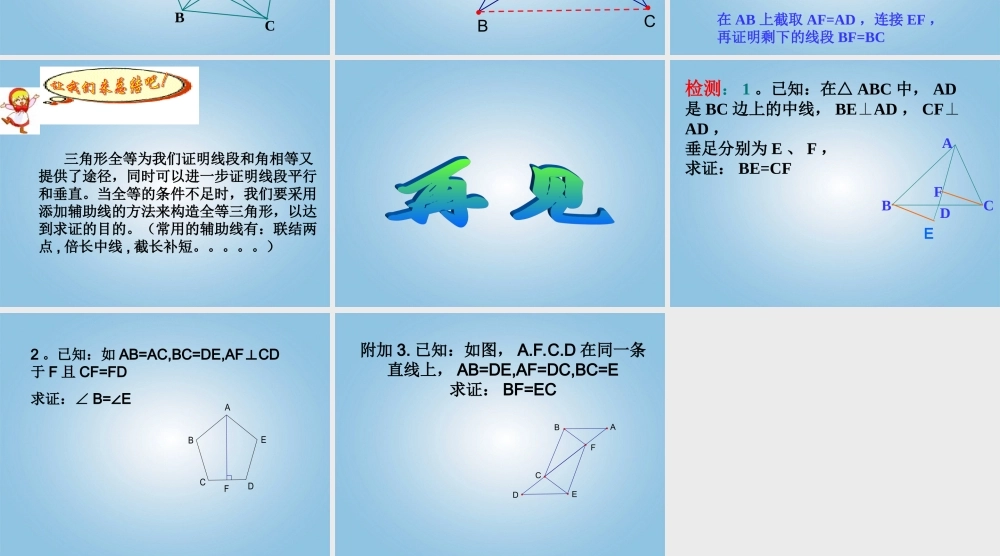
全等三角形复习课我们已学了三角形全等的哪些方法?三条边( SSS )两边夹角( SAS )两角夹边( ASA )两角一对边( AAS )1 如图,要判定△ ABCABD≌△,已具备一个条件是 ,应添加两个条件。( 1 ) 和 。 4ABCD123( 2 ) 和 。( SAS )( 3 ) 和 。( SAS )( 4 ) 和 。( ASA )( 5 ) 和 。( AAS )( 6 ) 和 。( AAS )AC=ADAB=ABBC=BDAC=AD∠1=2∠∠3=4∠BC=BD∠3=4∠∠1=2∠∠1=2∠∠C=D∠∠3=4∠∠C=D∠( SSS )斜边和直角边( HL )1. 已知:如图, ABBC⊥, ADDC⊥,垂足分别为 B 、 D , AC 平分∠BCD ,求证: BC=DCBCDA2. 如图, AB=AC , BDAC⊥,CEAB⊥,垂足分别为 D 、 E , BD 与 CE 相交于点 F ,求证: BE=CD 。BCEADF3 .已知:如图,点 E 、 F 在 AB 上, CAAB⊥于点 A , DBAB⊥于点 B , AE=BF,CF=DE求证: CF ED∥EABCFD∟∟我能行 以△ ABC 的 AB 和 AC 为边长分别在图形外作等边△ ABD 和等边 △ ACE ,连结 DC 、 BE 。求证: DC=BE 。ABCDE 试一试:已知 : 如图 ,AC 、 BD 交于点 O ,且 AB=CD , AC=BD 求证:∠ A= D∠DCOBA 如图, ADBC∥,∠ 1=2∠ , ∠ 3=4∠ ,直线 DC 过点 E 交 AD 于 D ,交 BC 于 C ,求证: AB=AD+BCFABCDE123 4分析:要证明一条线段等于另两条线段的和,我们往往在长的线段上截取一条线段等于较短线段中的一条。然后再设法证明剩下的线段等于另一条线段。在 AB 上截取 AF=AD ,连接 EF ,再证明剩下的线段 BF=BC 三角形全等为我们证明线段和角相等又提供了途径,同时可以进一步证明线段平行和垂直。当全等的条件不足时,我们要采用添加辅助线的方法来构造全等三角形,以达到求证的目的。(常用的辅助线有:联结两点 , 倍长中线 , 截长补短。。。。。)DABCF检测: 1 。已知:在△ ABC 中, AD是 BC 边上的中线, BEAD⊥, CF⊥AD ,垂足分别为 E 、 F ,求证: BE=CFE2 。已知:如 AB=AC,BC=DE,AFCD⊥于 F 且 CF=FD求证:∠ B= E∠FEDCBA附加 3. 已知:如图, A.F.C.D 在同一条直线上, AB=DE,AF=DC,BC=E求证: BF=ECFEDCBA