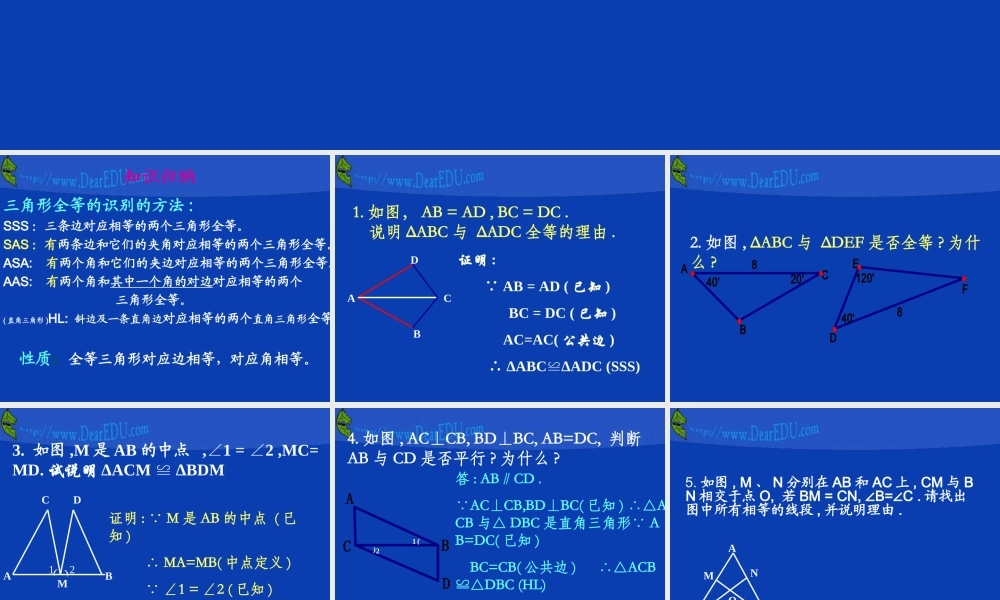
全等三角形(复习)知识归纳三角形全等的识别的方法 :SSS :三条边对应相等的两个三角形全等。SAS :有两条边和它们的夹角对应相等的两个三角形全等。ASA: 有两个角和它们的夹边对应相等的两个三角形全等。AAS: 有两个角和其中一个角的对边对应相等的两个 三角形全等。( 直角三角形 )HL: 斜边及一条直角边对应相等的两个直角三角形全等。 性质:全等三角形对应边相等,对应角相等。1. 如图, AB = AD , BC = DC . 说明 ΔABC 与 ΔADC 全等的理由 .CADB 证明 : ∵ AB = AD ( 已知 ) BC = DC ( 已知 ) AC=AC( 公共边 ) ∴ ΔABCΔADC (SSS)≌88120'20'40'40'FEDCBA2. 如图 , ΔABC 与 ΔDEF 是否全等 ? 为什么 ?3. 如图 ,M 是 AB 的中点 ,∠1 = ∠2 ,MC=MD. 试说明 ΔACM ≌ ΔBDMABMCD()12证明 : ∵ M 是 AB 的中点 ( 已知 ) ∴ MA=MB( 中点定义 ) ∵ ∠1 = ∠2 ( 已知 ) MC=MD( 已知 ) ∴ΔACM ≌ ΔBDM (SAS)4. 如图 , AC⊥CB, BD⊥BC, AB=DC, 判断AB 与 CD 是否平行 ? 为什么 ?DCBA答 : AB∥CD .∵AC⊥CB,BD⊥BC( 已知 ) ∴△ACB 与△ DBC 是直角三角形∵ AB=DC( 已知 ) BC=CB( 公共边 ) ∴△ACB≌△DBC (HL) ∴∠1=∠2( 全等三角形对应角相等 )∴ AB∥CD( 内错角相等 , 两直线平行 )()12 5. 如图 , M 、 N 分别在 AB 和 AC 上 , CM 与 BN 相交于点 O, 若 BM = CN, B= C .∠∠请找出图中所有相等的线段 , 并说明理由 . COBAMN 6. 如图,已知 AB = AC, 请问 : 再加一个什么条件就可以证得 ΔABE ΔACF,≌并说出它们的依据。 ABCEF解:∵ AB = AC ( 已知) ∴∠B = ∠C ( 等腰三角形两底角相等) 三 . 小结 1. 正确掌握每种识别方法中的 不同条件,并能准确应用它们; 2. 证明两三角形全等往往不是题目的最终目的,而是通过证明 两三角形全等得到它们的对应边、对应角相等; 3. 证题的方法不是唯一的,从结论出发去寻找证题的思路, 这种逆向思维的方法也是证明几何题的一种重要方法 . 附加题 : 已知: ΔABC 和 ΔBDE 是等边三角形 , 点 D 在 AE 的延长线上。 求证: BD + DC = AD ABCDE分析:∵ AD = AE + ED ∴ 只需证: BD + DC = AE + ED ∵BD = ED ∴ 只需证 DC = AE 即可。