数学人教版必修4A函数的图象及基本性质ppt 课件VIP免费

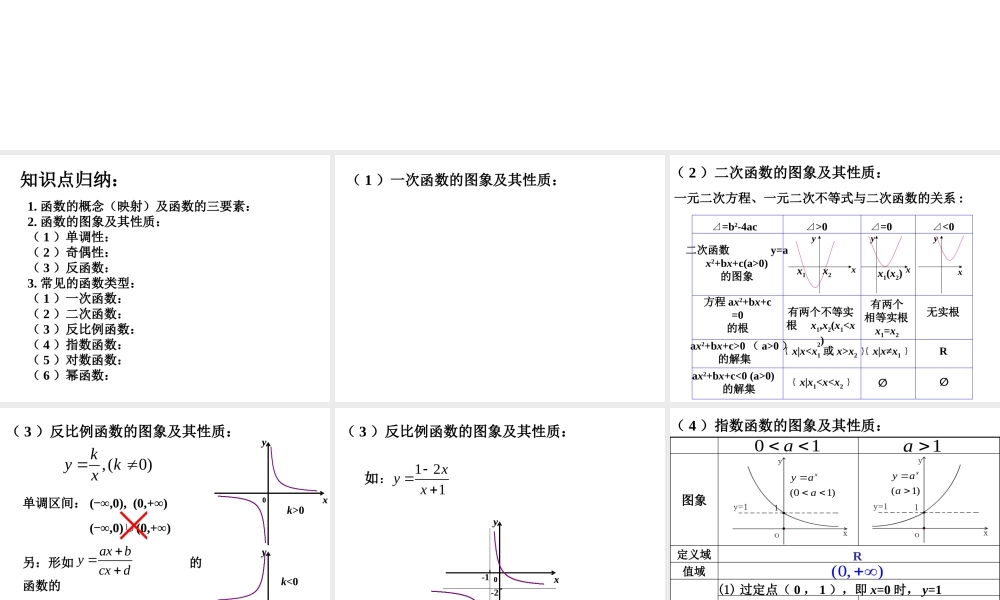
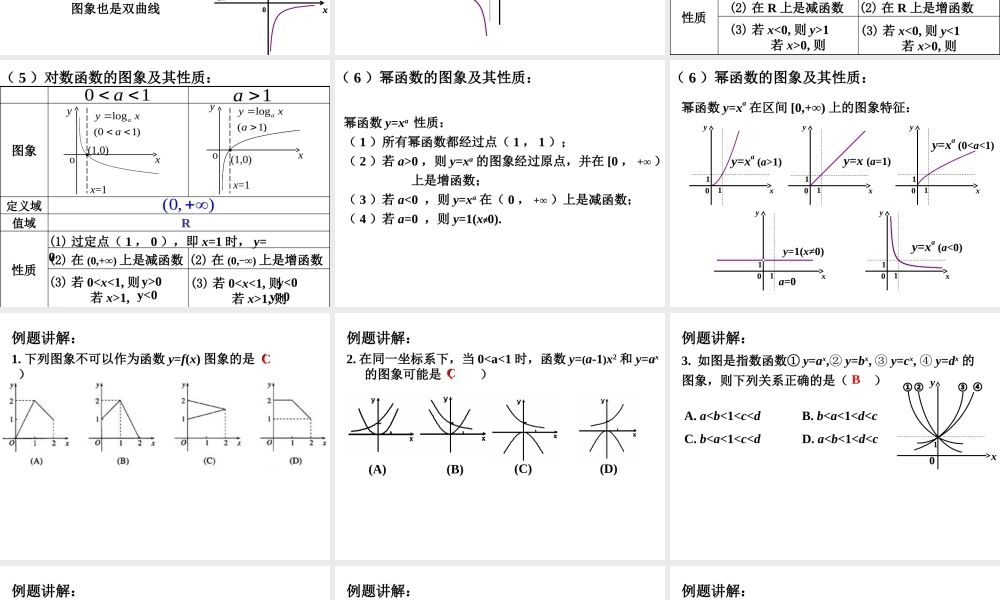
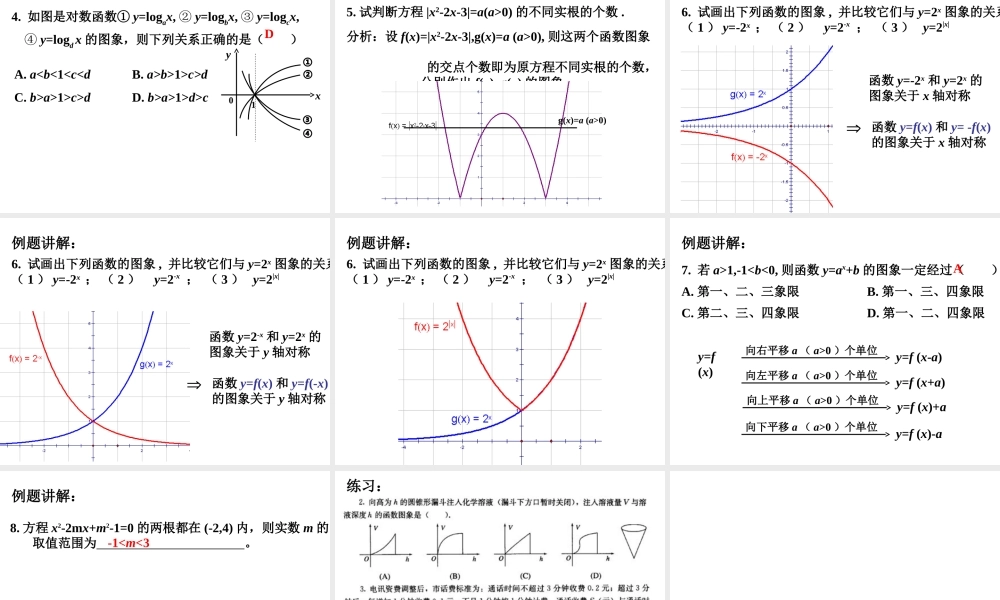
函数的图象及其基本性质 知识点归纳：1. 函数的概念（映射）及函数的三要素：2. 函数的图象及其性质：（ 1 ）单调性：（ 2 ）奇偶性：（ 3 ）反函数：3. 常见的函数类型：（ 1 ）一次函数：（ 2 ）二次函数：（ 3 ）反比例函数：（ 4 ）指数函数：（ 5 ）对数函数：（ 6 ）幂函数： （ 1 ）一次函数的图象及其性质： ⊿=b2-4ac二次函数 y=ax2+bx+c(a>0)的图象方程 ax2+bx+c=0的根ax2+bx+c>0 （ a>0 ） 的解集 ax2+bx+c<0 (a>0) 的解集⊿>0⊿=0⊿<0x1x2xyxx1(x2)yxy一元二次方程、一元二次不等式与二次函数的关系 :（ 2 ）二次函数的图象及其性质：有两个不等实根 x1,x2(x1x2﹜﹛x|x10xy0xy0k<0单调区间： (-∞,0), (0,+∞)(-∞,0)∪(0,+∞)另：形如 的函数的 图象也是双曲线 axbycxd 1 232(1)32111xxyxxx：如（ 3 ）反比例函数的图象及其性质：-1-2xy0xy0 性质值域定义域图象(01)xyaa(1)xyaa01a1a R(0,)(1) 过定点（ 0 ， 1 ），即 x=0 时， y=1(2) 在 R 上是减函数(2) 在 R 上是增函数(3) 若 x<0, 则 y>1 若 x>0, 则y<1(3) 若 x<0, 则 y<1 若 x>0, 则y>1（ 4 ）指数函数的图象及其性质： 性质值域定义域图象01a1a R(0,)(1) 过定点（ 1 ， 0 ），即 x=1 时， y=0(2) 在 (0,+∞) 上是减函数 (2) 在 (0,-∞) 上是增函数(3) 若 01,则(3) 若 01, 则y>0y<0y<0y>0oxyx=1(1,0)log(1)ayxaoxyx=1(1,0)log(01)ayxa（ 5 ）对数函数的图象及其性质： （ 6 ）幂函数的图象及其性质：幂函数 y=xa 性质：（ 1 ）所有幂函数都经过点（ 1 ， 1 ）；（ 2 ）若 a>0 ，则 y=xa 的图象经过原点，并在 [0 ， +∞ ） 上是增函数；（ 3 ）若 a<0 ，则 y=xa 在（ 0 ， +∞ ）上是减函数；（ 4 ）若 a=0 ，则 y=1(x≠0). y=xa (a>1)0xy1111y=x (a=1)0xy0xy11y=xa (0