北京市东城区普通高中示范校2013届高三12月综合练习(一)数学文试题VIP免费

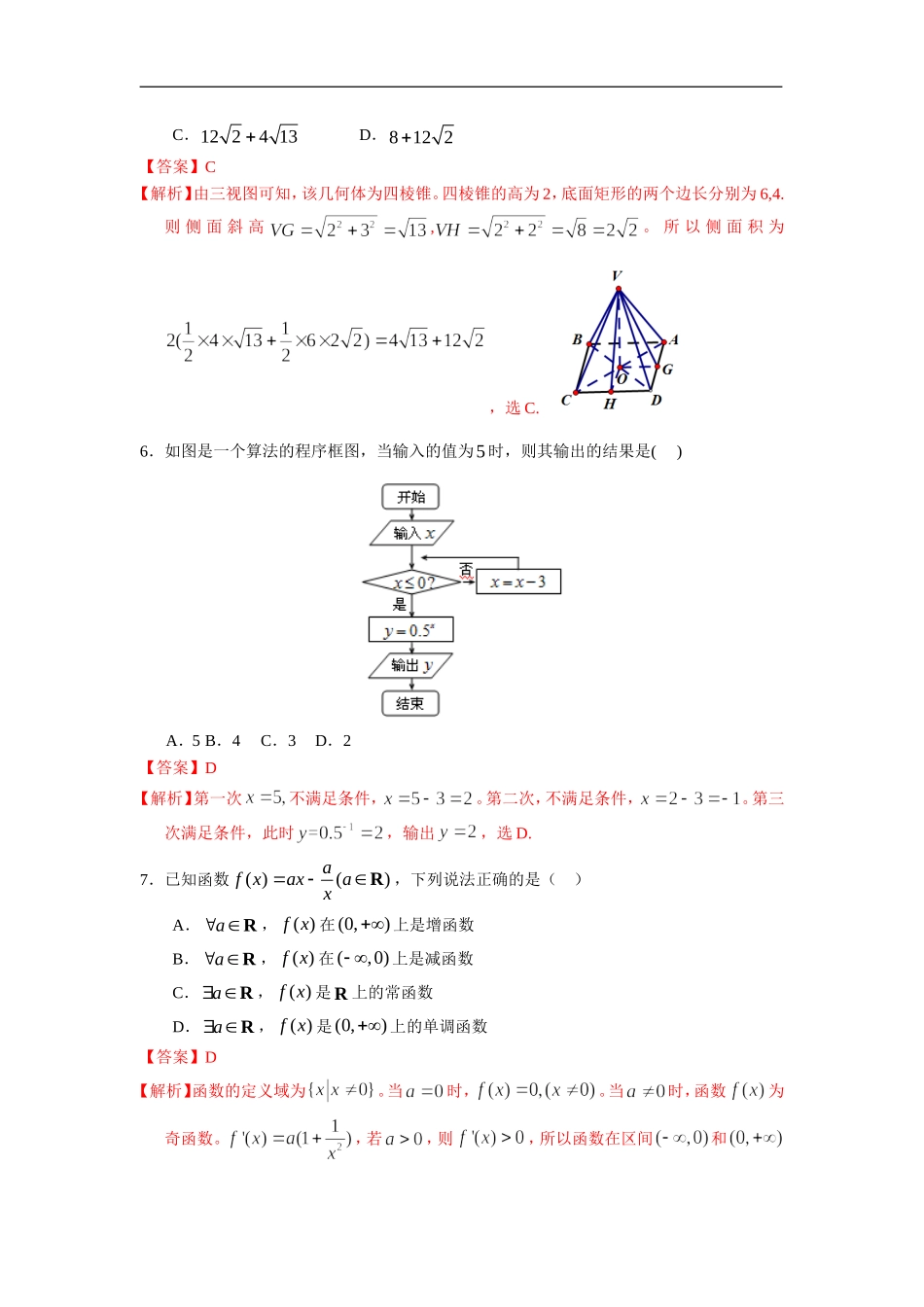
北京市东城区普通高中示范校2013届高三综合练习（一）数学试卷（文科）第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。1．设集合{1,2,3,4},{|||2,}PQxxxR，则PQ等于（）A．{1}B．{1,2}C．{3,4}D．{2,1,0,1,2}【答案】B【解析】,所以,所以选B.2．复数81i()1i的值是（）A．2iB．1iC．1iD．1【答案】D【解析】，所以，选D.3．下面四个条件中，使ab成立的充分不必要条件为（）A．1abB．1abC．22abD．33ab【答案】A【解析】因为，所以是成立的一个充分不必要条件，选A.4．已知向量(1,)xa，(1,)xb，若2ab与b垂直，则||a()A．2B．3C．2D．4【答案】C【解析】由题意知，因为与垂直，所以，即，所以，解得，所以，选C.5．某一棱锥的三视图如图所示，则其侧面积为()A．8413B．20C．122413D．8122【答案】C【解析】由三视图可知，该几何体为四棱锥。四棱锥的高为2，底面矩形的两个边长分别为6,4.则侧面斜高,。所以侧面积为，选C.6．如图是一个算法的程序框图，当输入的值为5时，则其输出的结果是()A．5B．4C．3D．2【答案】D【解析】第一次不满足条件，。第二次，不满足条件，。第三次满足条件，此时，输出，选D.7．已知函数()()afxaxaxR，下列说法正确的是（）A．aR，()fx在(0,)上是增函数B．aR，()fx在(,0)上是减函数C．aR，()fx是R上的常函数D．aR，()fx是(0,)上的单调函数【答案】D【解析】函数的定义域为。当时，。当时，函数为奇函数。，若，则，所以函数在区间和上，函数递增。若，则，所以函数在区间和上，函数递减。所以D正确，选D.8．如图，已知在四棱锥PABCD中，底面ABCD是菱形,PA底面ABCD，1,ABπ1,(0)2PAACABC，则四棱锥PABCD的体积V的取值范围是（）A．21[,)63B．21(,]126C．21(,]63D．21[,)126【答案】A【解析】，所以，所以高,底面积为,所以四棱锥的体积为，因为，所以，，即，所以体积的取值范围是，选A.第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分．9．若实数,xy满足不等式组2,24,0,xyxyxy则的最小值是__________．【答案】4【解析】做出不等式对应的可行域，由得，作直线，平移直线，由图象可知当直线经过点时，直线的截距最小，此时最小，最小为。如图10.公比为2的等比数列na的各项都为正数，且2616aa，则4a_______；12310aaaa_________________.【答案】4；10232【解析】由，解得。又，所以，所以.11．已知ABC的内角,,ABC所对的边分别为,,abc，且2a，3b，4cos5B，则sinA的值为__________．【答案】25【解析】因为,所以，根据正弦定理得。12．设)(xf是定义在R上的奇函数，当时，，且1()02f，则不等式的解集为__________．【答案】【解析】因为函数为奇函数。当时，，函数单调递增，所以，由图象可知，不等式的解为或，即不等式的解集为。13．已知直线:l20xy和圆:C221212540xyxy,则与直线l和圆C都相切且半径最小的圆的标准方程是_______________．【答案】【解析】圆C的标准方程为，圆心半径为。圆心C当直线的距离，则圆上的点到直线的最短距离为，要使圆与直线l和圆C都相切且半径最小，则圆的直径。所以所求圆心在直线上，且圆心到直线的距离为，解得圆心坐标为，所以圆的标准方程为。如图14．已知点(,)Pab与点(1,0)Q在直线2310xy的两侧，给出下列命题：①2310ab；②0a时，ba有最小值，无最大值；③存在正实数m，使得22abm恒成立；④0a且1a，0b时,则1ba的取值范围是12(,)(,)33.其中正确的命题是__________（把你认为所有正确的命题的序号都填上）．【答案】③④【解析】因为点P,Q在直线的两侧，所以，即，所以①错误。当时，得，即，所以无最小值，所以②错误。的几何意义为点到原点的距离。则原点到直线的距离，所以,所以只要，则有成立，所以③正确，如图.的几何意义表示点到点连线斜率的取值范围。由图象可知或，即的取...