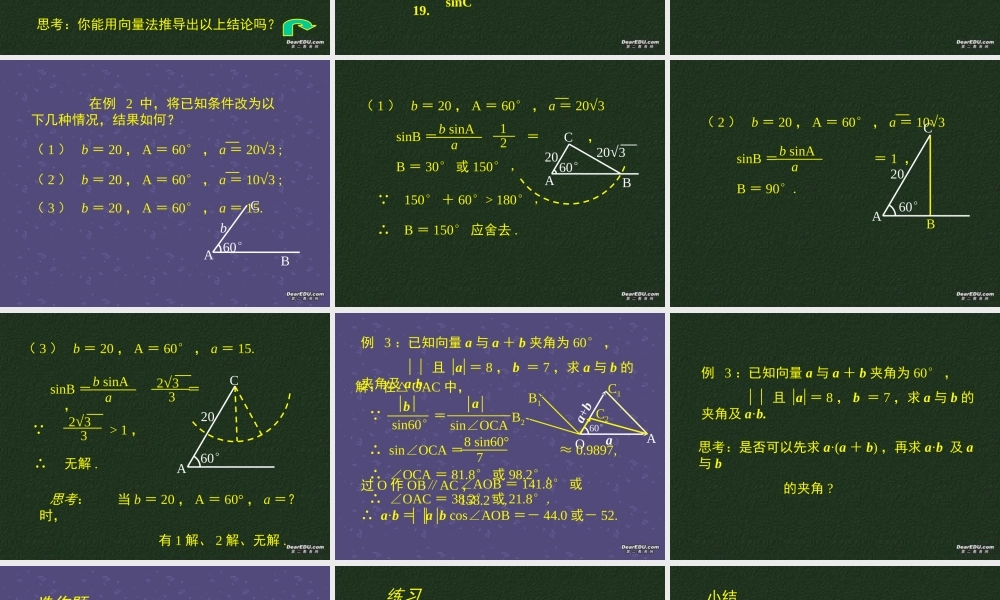
正弦定理怎样解直角三角形?已知两边;已知一边及一锐角 .sinA = , sinB = ,acbc = = . asinAbsinBcsinCABCabc怎样解斜三角形? 在一个三角形中各边和它所对角的正弦的比相等 . = = asinAbsinBcsinC =正弦定理? = = asinAbsinBcsinC= 2R.=2RbsinBB`ABCbOABCbOB`ABCbO思考:你能用向量法推导出以上结论吗?例 1 在 ABC 中,已知 c = 10 , A = 45° , C = 30° ,求 b.解: = , bsinBcsinCB=180°– (A + C) =105° ,ABCcbb = ≈19.c sinBsinC∴例 2 在 ABC 中,已知 a = 20 , b = 28 , A = 40° ,求 B 和 c.解: sinB = ≈ 0.8999b sinA a∴ B1 = 64° , B2 =116°40°ABCbB1B2······ 在例 2 中,将已知条件改为以下几种情况,结果如何?( 1 ) b = 20 , A = 60° , a = 20√3 ;( 2 ) b = 20 , A = 60° , a = 10√3 ;( 3 ) b = 20 , A = 60° , a = 15.60°ABCb( 1 ) b = 20 , A = 60° , a = 20√3sinB = = ,b sinA a12B = 30° 或 150° , 150° + 60°> 180° ,∴ B = 150° 应舍去 .60°2020√3ABC( 2 ) b = 20 , A = 60° , a = 10√3sinB = = 1 ,b sinA aB = 90°.B60°AC20( 3 ) b = 20 , A = 60° , a = 15.sinB = = ,b sinA a2√332√33 > 1 ,∴ 无解 .60°20AC 思考: 当 b = 20 , A = 60° , a =?时, 有 1 解、 2 解、无解 .例 3 :已知向量 a 与 a + b 夹角为 60° , 且 a = 8 , b = 7 ,求 a 与 b 的夹角及 a·b.解:在 OAC 中,bsin60°asin∠OCA =∴ sin∠OCA = ≈ 0.9897,8 sin60° 7∴ ∠OCA = 81.8° 或 98.2°,∴ ∠OAC = 38.2° 或 21.8°,过 O 作 OB∥AC ,∠AOB = 141.8° 或158.2°,∴ a·b = a b cos∠AOB =- 44.0 或- 52.60°aa+bOAC1C2B1B2例 3 :已知向量 a 与 a + b 夹角为 60° , 且 a = 8 , b = 7 ,求 a 与 b 的夹角及 a·b.思考:是否可以先求 a·(a + b) ,再求 a·b 及 a与 b 的夹角 ?选作题 如图,墙上有一个三角形灯架...