北京市海淀区2013届高三第二学期期中练习数学文试题(WORD版)VIP免费

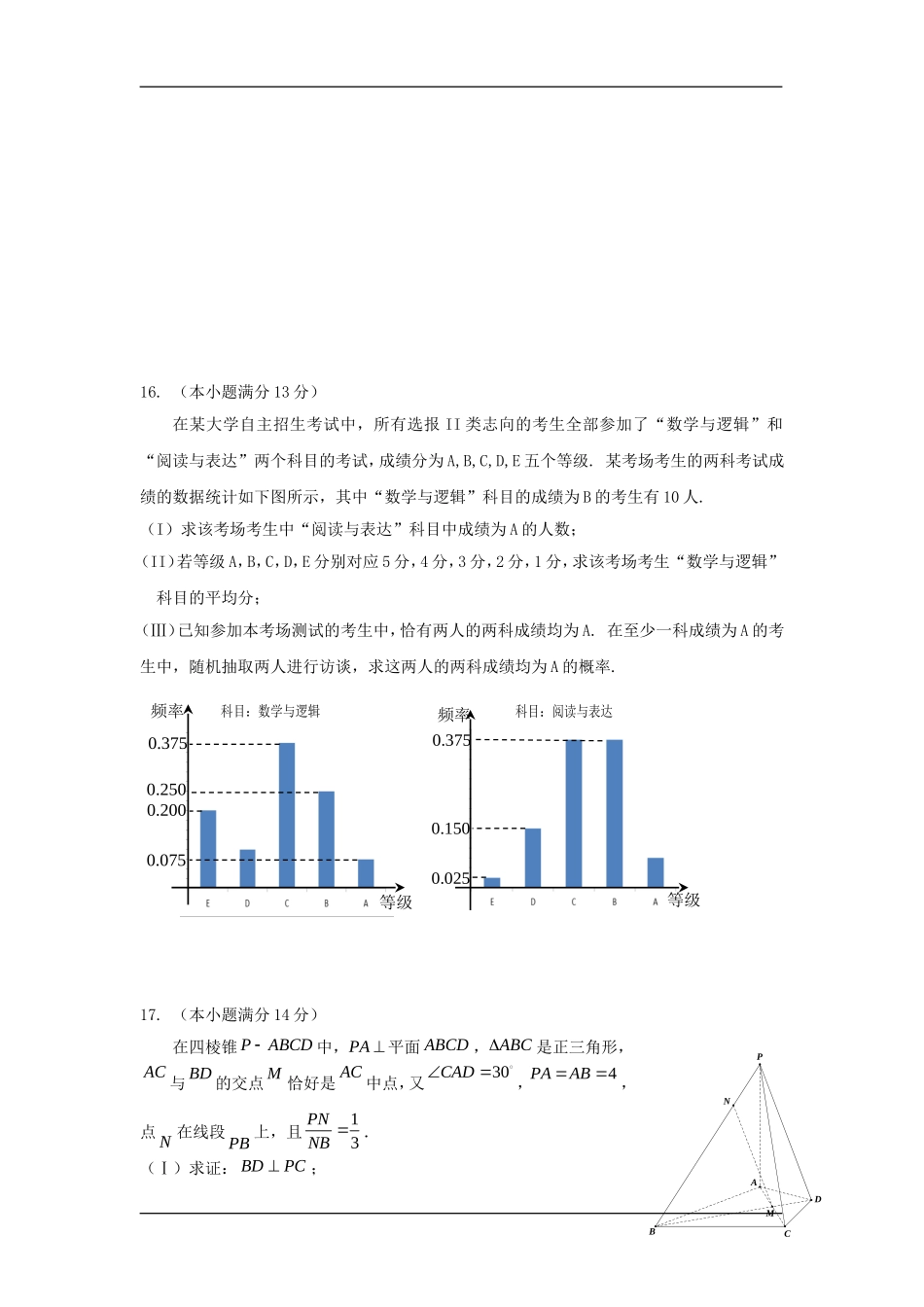
海淀区高三年级第二学期期中练习数学（文科）2013.4本试卷共4页，150分。考试时长120分钟。考生务必将答案答在答题卡上，在试卷上作答无效。考试结束后，将本试卷和答题卡一并交回。一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.集合2{6},{30}AxxBxxxN|N|，则ABA.{1,2}B.{3,4,5}C.{4,5,6}D.{3,4,5,6}2.等差数列{}na中,2343,9,aaa则16aa的值为A.14B.18C.21D.273.某程序的框图如图所示，执行该程序，若输入的x值为5，则输出的y值为Ａ.12B.1C.2D.14.已知0a，下列函数中，在区间(0,)a上一定是减函数的是Ａ.()fxaxbB.2()21fxxaxC.()xfxaD.()logafxx5.不等式组1,40,0xxykxy表示面积为1的直角三角形区域，则k的值为A.0B.1C.2D.36.命题:p,Rsin(π)cos；命题:q0,m双曲线22221xymm的离心率为2.则下面结论正确的是A.p是假命题B.q是真命题C.pq是假命题D.pq是真命题7.已知曲线()lnfxx在点00(,())xfx处的切线经过点(0,1)，则0x的值为Ａ.1eB.1C.eD.10开始输出y结束输入x2xx0xxy2是否8.抛物线24yx的焦点为F，点P为抛物线上的动点，点M为其准线上的动点，当FPM为等边三角形时，其面积为A.23B.4C.6D.43二、填空题:本大题共6小题,每小题5分,共30分.9.在复平面上，若复数1+ib（bR）对应的点恰好在实轴上，则b=_______.10.若向量,ab满足||||||1abab，则ab的值为______.11.某几何体的三视图如图所示，则它的体积为______.12.在ABC中，若4,2,ab1cos4A，则______.c13.已知函数22,0,(),0xaxfxxaxax有三个不同的零点，则实数a的取值范围是_____.14.已知函数()yfx，任取tR，定义集合:{|tAy()yfx，点(,())Ptft，(,())Qxfx满足||2}PQ.设,ttMm分别表示集合tA中元素的最大值和最小值，记()tthtMm.则(1)若函数()fxx，则(1)h=______;（2）若函数π()sin2fxx，则()ht的最小正周期为______.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.（本小题满分13分）已知函数2()2(3sincos)fxxx.（Ⅰ）求π()3f的值和()fx的最小正周期；（Ⅱ）求函数在区间ππ[,]63上的最大值和最小值.俯视图24侧视图主视图2224416.（本小题满分13分）在某大学自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分为A,B,C,D,E五个等级.某考场考生的两科考试成绩的数据统计如下图所示，其中“数学与逻辑”科目的成绩为B的考生有10人.（I）求该考场考生中“阅读与表达”科目中成绩为A的人数；（II）若等级A，B，C，D，E分别对应5分，4分，3分，2分，1分，求该考场考生“数学与逻辑”科目的平均分；（Ⅲ）已知参加本考场测试的考生中，恰有两人的两科成绩均为A.在至少一科成绩为A的考生中，随机抽取两人进行访谈，求这两人的两科成绩均为A的概率.0.375等级0.250频率0.2000.075科目：数学与逻辑0.025频率等级0.1500.375科目：阅读与表达17.（本小题满分14分）在四棱锥PABCD中，PA平面ABCD，ABC是正三角形，AC与BD的交点M恰好是AC中点，又30CAD，4PAAB，点N在线段PB上，且13PNNB．（Ⅰ）求证：BDPC；MDCBAPN（Ⅱ）求证：//MN平面PDC；（Ⅲ）设平面PAB平面PCD=l，试问直线l是否与直线CD平行，请说明理由.18.（本小题满分13分）函数31()3fxxkx,其中实数k为常数.(I)当4k时，求函数的单调区间；(II)若曲线()yfx与直线yk只有一个交点，求实数k的取值范围.19.（本小题满分14分）已知圆M：227(2)3xy,若椭圆C：22221xyab（0ab）的右顶点为圆M的圆心，离心率为22.（I）求椭圆C的方程；（II）已知直线l：ykx，若直线l与椭圆C分别交于A，B两点，与圆M分别交于G，H两点（其中点G在线段AB上），且AGBH，求k的值.20.（本小题满分13分）设(,),(,)AABBAxyBxy为平面直角坐标系上的两点，其中,,,AABBxyxyZ.令BAxxx，BAyyy，若x+=3y,且||||0xy，则称点B为点A的...