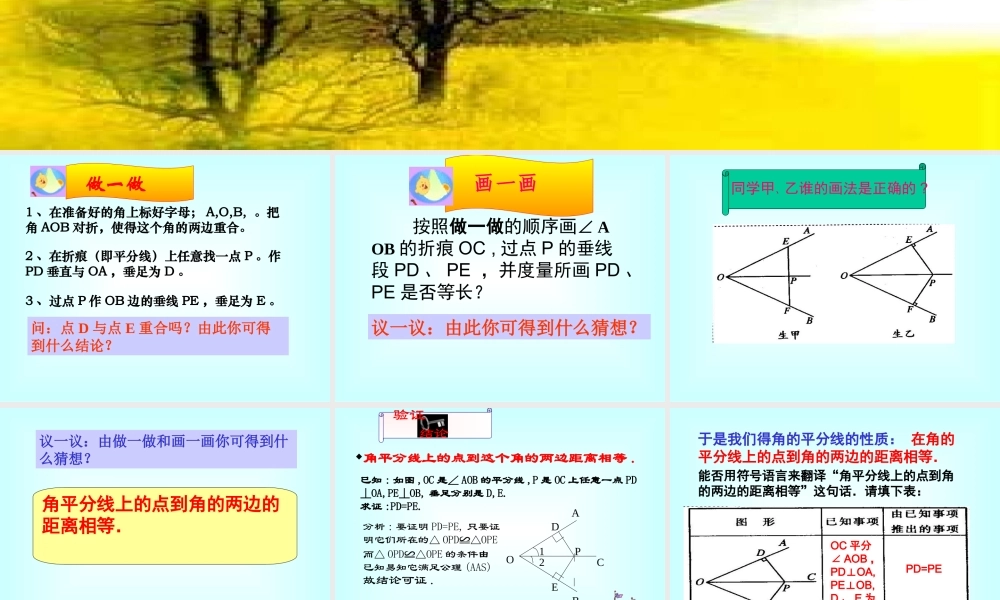
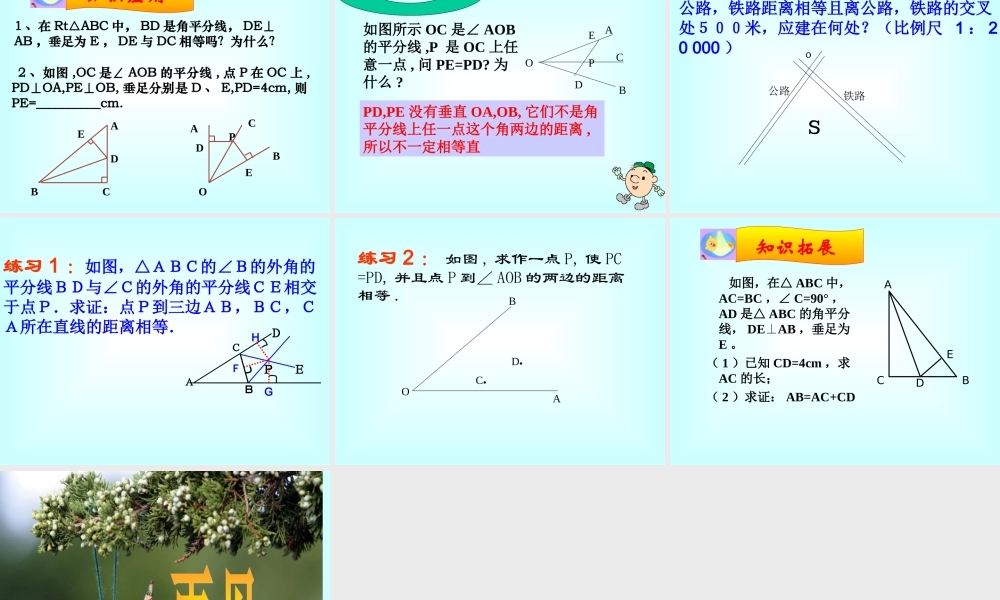
1 、在准备好的角上标好字母; A,O,B, 。把角 AOB 对折,使得这个角的两边重合。2 、在折痕(即平分线)上任意找一点 P 。作PD 垂直与 OA ,垂足为 D 。3 、过点 P 作 OB 边的垂线 PE ,垂足为 E 。做一做问:点 D 与点 E 重合吗?由此你可得到什么结论? 按照做一做的顺序画∠ AOB 的折痕 OC , 过点 P 的垂线段 PD 、 PE ,并度量所画 PD 、PE 是否等长?议一议:由此你可得到什么猜想?画一画 同学甲、乙谁的画法是正确的 ? 角平分线上的点到角的两边的距离相等. 议一议:由做一做和画一画你可得到什么猜想? 验证 结论已知 : 如图 ,OC 是∠ AOB 的平分线 ,P 是 OC 上任意一点 PD⊥OA,PE⊥OB, 垂足分别是 D,E.求证 :PD=PE.而△ OPD≌△OPE 的条件由已知易知它满足公理 (AAS). 故结论可证 .老师期望 : 你能写出规范的证明过程 .分析 : 要证明 PD=PE, 只要证明它们所在的△ OPD≌△OPE,角平分线上的点到这个角的两边距离相等 .OCB1A2PDE 能否用符号语言来翻译“角平分线上的点到角的两边的距离相等”这句话.请填下表:PD=PEOC 平分∠ AOB ,PDOA, ⊥PEOB, ⊥D 、 E 为垂足.于是我们得角的平分线的性质: 在角的平分线上的点到角的两边的距离相等. 到角的两边距离相等的点是否在角的平分线上呢?议 一 议 根据下表中的图形和已知事项,猜想由已知事项可推出的事项,并用符号语言填写下表:点 P 在∠ AOB的平分线上 这样,我们又可以得到一个结论: 到角的两边距离相等的点在角的平分线上。请同学们自己写出证明过程 同学们思考一下,这节课所学的这两个性质有什么联系吗? 例 已知:如图,△ ABC 的角平分线 BM 、 CN 相交于点 P.求证:点 P 到三边 AB 、 BC 、 CA 的距离相等 .ABCP MNABCP MN例 已知:如图,△ ABC 的角平分线 BM 、 CN 相交于点 P.求证:点 P 到三边 AB 、 BC 、 CA 的距离相等 .证明:过点 P 作 PD 、 PE 、 PF 分别垂直于 AB 、 BC 、 CA ,垂足分别为 D 、 E 、 FFDEDE BM 是△ ABC 的角平分线,点 P 在 BM 上 ∴PD=PE (在角平分线上的点到角的两边 的距离相等) 同理 PE=PF. ∴ PD=PE=PF. 即点 P 到边 AB 、 BC 、 CA 的距离相等想一想,点 P 在∠ A 的 平分线上吗?这说明三角形的三条角平分线有什么关系? 畅 谈 收...