初三数学几何综合题及答案VIP免费

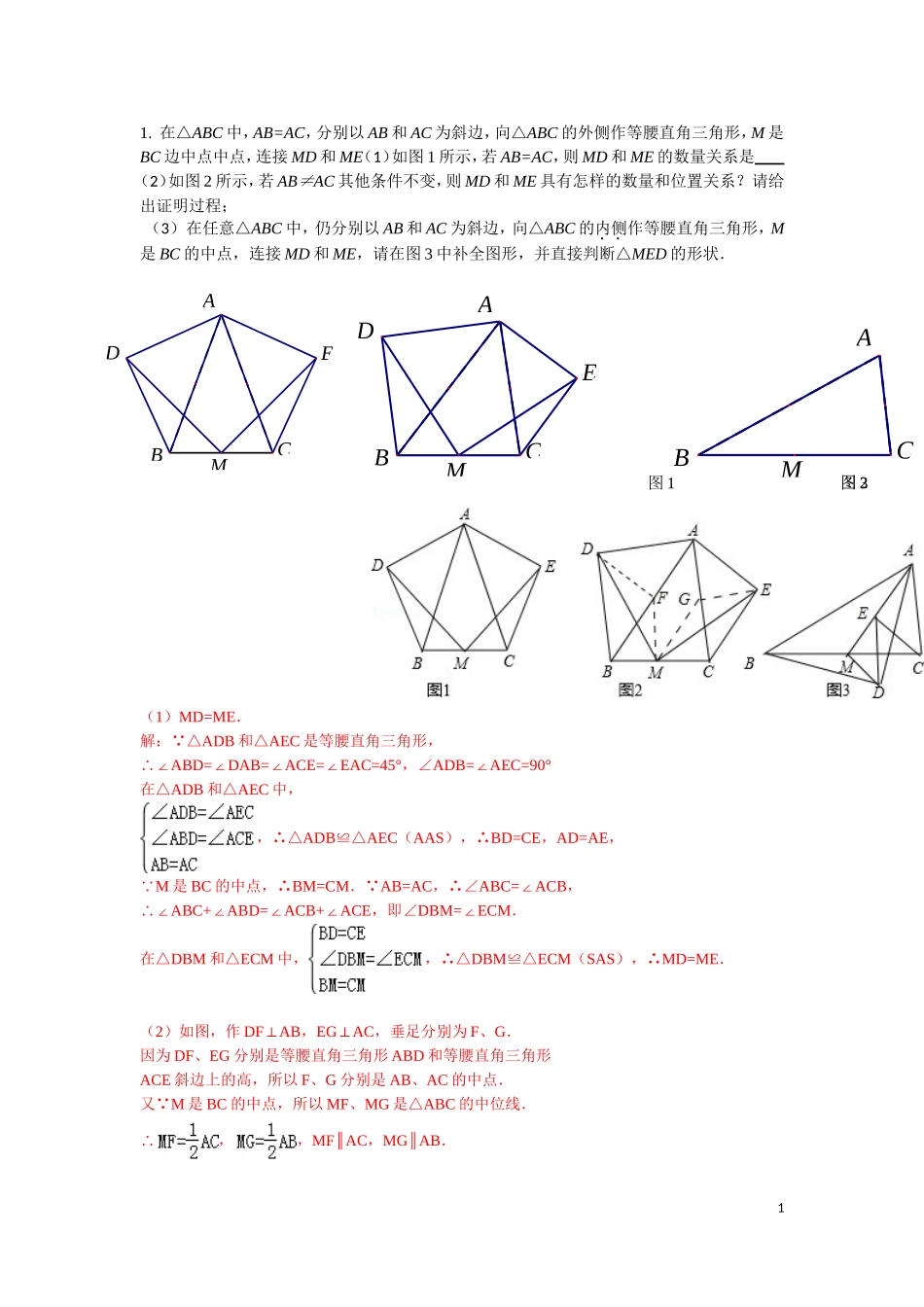
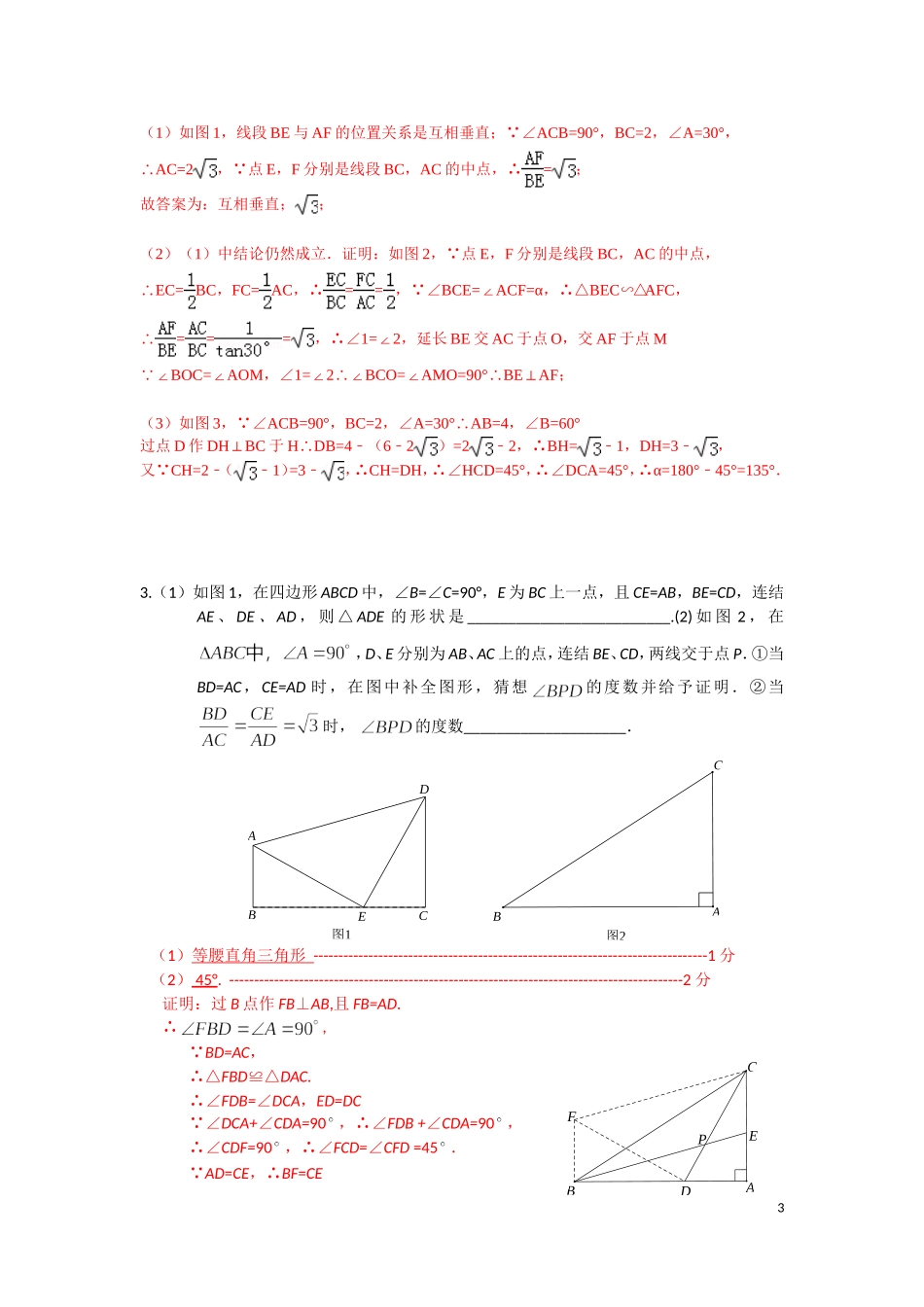
EDMBCAEDMBCAMBCA1.在△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，M是BC边中点中点，连接MD和ME（1）如图1所示，若AB=AC，则MD和ME的数量关系是（2）如图2所示，若AB≠AC其他条件不变，则MD和ME具有怎样的数量和位置关系？请给出证明过程；（3）在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，M是BC的中点，连接MD和ME，请在图3中补全图形，并直接判断△MED的形状．（1）MD=ME．解： △ADB和△AEC是等腰直角三角形，ABD=DAB=ACE=EAC=45°∴∠∠∠∠，∠ADB=AEC=90°∠在△ADB和△AEC中，，∴△ADBAEC≌△（AAS），∴BD=CE，AD=AE，M 是BC的中点，∴BM=CM． AB=AC，∴∠ABC=ACB∠，ABC+ABD=ACB+ACE∴∠∠∠∠，即∠DBM=ECM∠．在△DBM和△ECM中，，∴△DBMECM≌△（SAS），∴MD=ME．（2）如图，作DFAB⊥，EGAC⊥，垂足分别为F、G．因为DF、EG分别是等腰直角三角形ABD和等腰直角三角形ACE斜边上的高，所以F、G分别是AB、AC的中点．又 M是BC的中点，所以MF、MG是△ABC的中位线．∴，，MFAC∥，MGAB∥．1图1图2图3BFM=BAC∴∠∠，∠MGC=BAC∠．∴∠BFM=MGC∠．所以∠DFM=MGE∠．DF 、EG分别是直角三角形ABD和直角三角形ACE斜边上的中线，∴，．∴MF=EG，DF=MG．在△DFM与△MGE中，，∴△DFMMGE≌△（SAS）．∴DM=ME．∠FMD=GEM∠DME=FMD+FMG+GME=GEM+MGC+GME∴∠∠∠∠∠∠∠EGACEGC=90° ⊥∴∠GEM+MGC+GME+EGC=180°DME=90° ∠∠∠∠∴∠DMEM∴⊥．（3）如图所示：MDE△是等腰直角三角形．2．如图1，在中，，，∠A=30°，点E，F分别是线段BC，AC的中点，连结EF．（1）线段与的位置关系是________，________．（2）如图2，当绕点顺时针旋转时（），连结AF，BE，（1）中的结论是否仍然成立.如果成立，请证明；如果不成立，请说明理由．（3）如图3，当绕点顺时针旋转时（），延长交于点，如果，求旋转角的度数．2DαFECBA图3图2αFECBAFECBA图1图2图1EDCBAABCPFEDABC（1）如图1，线段BE与AF的位置关系是互相垂直； ∠ACB=90°，BC=2，∠A=30°，AC=2∴， 点E，F分别是线段BC，AC的中点，∴=；故答案为：互相垂直；；（2）（1）中结论仍然成立．证明：如图2， 点E，F分别是线段BC，AC的中点，EC=∴BC，FC=AC，∴==， ∠BCE=ACF=α∠，∴△BECAFC∽△，∴===，∴∠1=2∠，延长BE交AC于点O，交AF于点MBOC=AOM ∠∠，∠1=2BCO=AMO=90°BEAF∠∴∠∠∴⊥；（3）如图3， ∠ACB=90°，BC=2，∠A=30°AB=4∴，∠B=60°过点D作DHBC⊥于HDB=4∴﹣（62﹣）=22﹣，∴BH=1﹣，DH=3﹣，又 CH=2﹣（﹣1）=3﹣，∴CH=DH，∴∠HCD=45°，∴∠DCA=45°，∴α=180°45°=135°﹣．3.（1）如图1，在四边形ABCD中，∠B=∠C=90°，E为BC上一点，且CE=AB，BE=CD，连结AE、DE、AD，则△ADE的形状是_________________________.(2)如图2，在，D、E分别为AB、AC上的点，连结BE、CD，两线交于点P．①当BD=AC，CE=AD时，在图中补全图形，猜想的度数并给予证明．②当时，的度数____________________．（1）等腰直角三角形-------------------------------------------------------------------------------1分（2）45°.-------------------------------------------------------------------------------------------2分证明：过B点作FB⊥AB,且FB=AD.∴, BD=AC，∴△FBD≌△DAC.∴∠FDB=∠DCA，ED=DC ∠DCA+∠CDA=90，∴∠FDB+∠CDA=90，∴∠CDF=90，∴∠FCD=∠CFD=45． AD=CE，∴BF=CE3 ，∴.∴BF∥EC.∴四边形BECF是平行四边形．∴BE∥FC.∴.-----------------------------------------------------------------------6分（3）60．--------------------------------------------------------------------------------------7分4．在△ABC中，ABAC，A0，将线段BC绕点B逆时针旋转60得到线段BD，再将线段BD平移到EF，使点E在AB上，点F在AC上．（1）如图1，直接写出ABD和CFE的度数；（2）在图1中证明：ECF；（3）如图2，连接CE，判断△CEF的形状并加以证明．1）ABD=15°，CFE=45°．………………………………………2分（2...